Уравнения узловых напряжений
Уравнения узловых напряжений (УУН) — система нелинейных (иногда линейных) алгебраических уравнений, в которых неизвестными являются напряжения в узлах электрической сети, наиболее часто применяемая для расчёта установившегося режима электрической сети.
Содержание
Описание
Установившийся режим электрических систем можно рассчитывать при различных способах задания исходных данных в зависимости от физической сути и цели расчёта. В статье рассмотрен наиболее часто встречающийся и наиболее простой случай, когда известны сопротивления и проводимости всех пассивных элементов электрической сети. Кроме того, заданы постоянные величины всех значений токов (мощности) во всех узлах, кроме балансирующего и все ЭДС, а также напряжение одного узла — базисного. При этом необходимо определить напряжения всех [math](n-1)[/math] узлов и токи во всех m ветвях.
В общем случае базисный по напряжению и балансирующий узлы могут не совпадать. Как правило, при расчётах режимов электрических систем предполагают, что эти узлы совпадают, в дальнейшем для простоты изложения предполагается, что базисным по напряжению и балансирующим является один и тот же [math]n[/math]-й узел. Число независимых уравнений по первому закону Кирхгофа равно числу независимых узлов [math](n-1)[/math]. Уравнение первого закона Кирхгофа для [math]n[/math]-го узла является следствием уравнений для остальных [math](n-1)[/math] узлов и не входит в число независимых уравнений.
Если в качестве неизвестных принять [math](n-1)[/math] узловых напря¬жений, то установившийся режим можно описать только узловыми уравнениями, вытекающими из первого закона Кирхгофа и закона Ома [1], [2], [3], [4]. Уравнения узловых напряжений следуют из первого закона Кирхгофа, если все токи в ветвях выразить через узловые напряжения и проводимости ветвей. Число уравнений узловых напряжений равно числу независимых узлов [math](n-1)[/math].
Уравнения баланса токов представляют собой простейшую форму уравнений, описывающих установившиеся режимы. Существуют две математические модели уравнений узловых напряжений:
- линейная;
- нелинейная.
Отличительной особенностью этих моделей является то, что линейная модель предполагает задание комплексных значений токов, в отличие от нелинейной модели, которая предполагает задание активной и реактивной мощностей. В большинстве задач нагрузки в узлах задаются активной и реактивной мощностями, по этой причине обычно используется нелинейная модель.
Каждый узел графа расчётной модели характеризуется 4 параметрами: активная (P) и реактивная (Q) мощность, модуль (V) и угол ([math]\delta[/math]) напряжения. В связи с тем, что каждого узла возможно составить только два независимых уравнения, то можно оценить только два парамтера из четырёх. Оставшиеся два параметра принимают в качестве исходных данных. В зависимости от того какие параметры приняты в качестве исходных данных принято различать:
- PV узел - задаётся активная мощность и модуль напряжения.
- PQ узел - задаётся активная и реактиная мощность.
- V[math]\delta[/math] узел - задаётся модуль и угол напряжения, обычно принимается в качестве базисного и балансирующего узла.
Вывод уравнений узловых напряжений
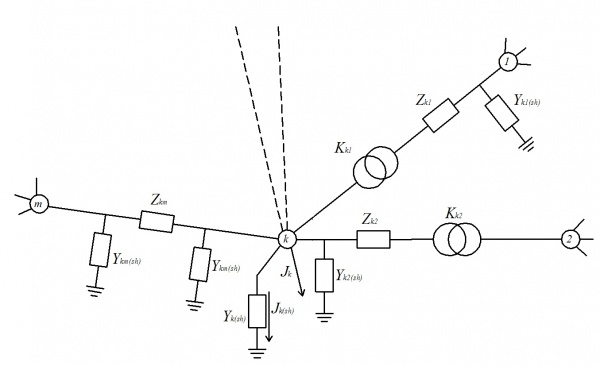
Для формирования УУН рассмотрим представленную на рис. 1 часть схемы замещения:
Первый закон Кирхгофа для к-го узла:
- [math]\displaystyle \dot{J_k}+\dot{J}_{k(sh)}+\sum_{m∈k}\dot{J}_{km(sh)}+\sum_{m∈k}\dot{J}_{km}=0,[/math]
- где [math]m \in k[/math] означает, что любой узел [math]m[/math] связан с узлом [math]k[/math];
- [math]\displaystyle \dot{J_k}[/math] — ток нагрузки в узле [math]k[/math];
- [math]\displaystyle \dot{J}_{k(sh)}[/math] — ток шунта, подключенного к узлу [math]k[/math];
- [math]\displaystyle \dot{J}_{km(sh)}[/math] — ток, протекающий через поперечные проводимости ЛЭП или трансформатора [math]km[/math], подсоединенные к узлу [math]k[/math];
- [math]\displaystyle \dot{J}_{km}[/math] — ток продольной ветви [math]km[/math] ЛЭП или трансформатора от узла [math]k[/math].
- ветвь, моделирующая шунтовые проводимости:
- [math]\displaystyle \dot{J}_{k(sh)}=\dot{U_k}\underline{Y}_{km(sh)},[/math]
- ветвь, не содержащая трансформаторов:
- [math]\displaystyle \dot{J}_{km}=\frac{\dot{U_k}-\dot{U_m}}{\underline{Z}_{km}},[/math]
- трансформаторная ветвь [math]k2[/math], сопротивление [math]\underline{Z}_{k2}[/math] которой приведено к узлу [math]k[/math]:
- [math]\displaystyle \dot{J}_{k2}=\frac{\dot{U_k}-\frac{\dot{U_2}}{\dot{k}_{k2}}}{\underline{Z}_{k2}},[/math]
- трансформаторная ветвь [math]k1[/math], сопротивление [math]\underline{Z}_{k1}[/math] которой приведено к смежному узлу [math]1[/math]:
- [math]\displaystyle \dot{J}_{k1}=\frac{1}{\hat{k}_{k1}}\frac{\frac{\dot{U_k}}{\dot{k}_{k1}}-\dot{U_1}}{\underline{Z}_{k1}}.[/math]
Наличие знака сопряжения в этом выражении обусловлено тем, что для идеального двухобмоточного трансформатора выполняется закон сохранения мощности [math]\dot{S_н}=\dot{S_в}=\hat{I_н}\dot{U_н}=\hat{I_в}\dot{U_в}[/math], где индексами «Н» и «В» обозначены соответственно низшая и высшая обмотки трансформатора, поэтому, если [math]\dot{U_в}=\dot{U_н}\dot{K_{вн}}[/math], то из закона сохранения следует:
- [math]\displaystyle \dot{I_в}=\dot{I_н}\frac{\hat{U_н}}{\hat{U_в}}=\frac{\dot{I_н}}{\hat{k}_{вн}}.[/math]
Подстановка полученных выражений в уравнение (1.1) с приведением подобных членов позволяет получить уравнение для k-го узла в виде:
- [math]\displaystyle \underline{y}_{ii}\dot{U_i}+\sum_{m∈k}\underline{y}_{ik}\dot{U_k}=\dot{I_k}[/math].
В прямоугольной системе координат
В данной системе комплексные величины [math]\displaystyle \underline{y}_{ik}, \dot{U_{j}}, \dot{J_{i}}[/math] представляются в виде
- [math]\displaystyle \dot{U_{k}}=U_{k}'+jU_{k}'',[/math]
- [math]\displaystyle \dot{J_{i}}=J_{i}'+jJ_{i}'',[/math]
для проводимости справедливо следующее:
- [math]\displaystyle \underline{y}=\frac{1}{\underline{z}}=\frac{1}{r+jx}=\frac{r-jx}{(r+jx)(r-jx)}=\frac{r-jx}{r^2+x^2}=\frac{r}{r^2+x^2}-j\frac{x}{r^2+x^2}=\frac{r}{|\underline{z}|^2}-j\frac{x}{|\underline{z}|^2} \Rightarrow g=\frac{r}{|\underline{z}|^2}; b=\frac{x}{|\underline{z}|^2},[/math]
получаем, что [math]\displaystyle \underline{y}=g-jb,[/math]
но для удобства расчёта матрицы проводимостей будем использовать соотношение
- [math]\displaystyle\underline{y}=g+jb[/math], тогда
- [math]\displaystyle \underline{y}_{ik}=g_{ik}+jb_{ik};[/math] [math]\underline{y}_{ii}=g_{ii}+jb_{ii};[/math]
- [math]\displaystyle g_{ii}=-\sum_{j=1,j\neq{i}}^Ng_{ik};[/math] [math]b_{ii}=-\sum_{j=1,j\neq{i}}^Nb_{ik}.[/math]
Запишем УУН для линейной ЭЭС:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N} \underline{Y}_{ik} \dot {U}_{k} = \dot{J}_{i} - \underline{Y}_{iб} \dot {U}_{б}, i=1 \ldots N\end{cases}, [/math]
левая часть данной системы характеризует токи, втекающие в k-й узел, правая часть — токи, вытекающие из того же узла, но с учетом влияния токов базы.
Подставляем (1), (2), (3) в (4), [math]\dot{U}_б[/math] представим аналогично уравнению (1), тогда имеем следующее:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N} \left( g_{ik} + j b_{ik} \right) \left( U_{k}' + j U_{k}'' \right) = J_{i}' + j J_{i}''- \left( g_{iб} + j b_{iб} \right) \left(U_{б}' + j U_{б}''\right), i = 1 \ldots N \end{cases}.[/math]
Сгруппируем и приведем подобные:
- [math]\displaystyle \begin{cases}\sum_{k=1}^{N}\left(\left(g_{ik}U_k'-b_{ik}U_k''\right)+j\left(g_{ik}U_k''+b_{ik}U_k'\right)\right)=J_{i}'+jJ_{i}''-\left(\left(g_{iб}U_б'-b_{iб}U_б''\right)+j\left(g_{iб}U_б''+b_{iб}U_б'\right)\right), i=1 \ldots N\end{cases}[/math].
Сгруппируем относительно [math]j[/math] левую и правую части системы (5). Два комплексных числа равны, если равны их действительные и мнимые составляющие. Распишем в новой системе отдельно действительные и мнимые части. Получаем:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N}\left(g_{ik}U_k'-b_{ik}U_k''\right)=J_{i}'-\left(g_{iб}U_б'-b_{iб}U_б''\right) \\ \sum_{k=1}^{N}\left(g_{ik}U_k''+b_{ik}U_k'\right)=J_{i}''-\left(g_{iб}U_б''+b_{iб}U_б'\right) \end{cases}, i=1 \ldots N.[/math]
Представим данную систему (6) в матричной форме:
- [math]\displaystyle \begin{pmatrix} \bar{\bar{G}} & -\bar{\bar{B}} \\ \bar{\bar{B}} & \bar{\bar{G}} \end{pmatrix} \begin{pmatrix} \bar{U'} \\ \bar{U''} \end{pmatrix}= \begin{pmatrix} \bar{J'} \\ \bar{J''} \end{pmatrix}- \begin{pmatrix} \bar{G_б} & -\bar{B_б} \\ \bar{B_б} & \bar{G_б} \end{pmatrix} \begin{pmatrix} \bar{U_б'} \\ \bar{U_б''} \end{pmatrix}. [/math]
В случае, если [math]\dot{U}_б=U_б+j0,[/math] система (6) преобразуется к виду:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N}\left(g_{ik}U_k'-b_{ik}U_k''\right)=J_{i}'-g_{iб}U_б, i=1 \ldots N\\ \sum_{k=1}^{N}\left(g_{ik}U_k''+b_{ik}U_k'\right)=J_{i}''-b_{iб}U_б, i=1 \ldots N \end{cases}.[/math]
Соответственно упрощается матричная форма записи системы (8):
- [math]\displaystyle \begin{pmatrix} \bar{\bar{G}} & -\bar{\bar{B}} \\ \bar{\bar{B}} & \bar{\bar{G}} \end{pmatrix} \begin{pmatrix} \bar{U'} \\ \bar{U''} \end{pmatrix}= \begin{pmatrix} \bar{J'} \\ \bar{J''} \end{pmatrix}- \begin{pmatrix} \bar{G_б} \\ \bar{B_б} \end{pmatrix} U_б .[/math]
Вернемся к нелинейной модели ЭЭС. Для этого перенесем составляющую токов базы системы (4) в левую часть, изменив при этом диапазон [math]i=1 \ldots (N-1)[/math]. Получаем:
- [math]\displaystyle \begin{cases}\sum_{k=1}^{N}\underline{Y}_{ik}\dot{U}_{k}=\dot{J}_{i}, i=1 \ldots (N-1)\end{cases}.[/math]
Как известно,
- [math]\displaystyle \dot{S}=\dot{U}\hat{J}[/math], отсюда [math]\hat{J}=\frac{\dot{S}}{\dot{U}}[/math] или [math]\dot{J}=\frac{\hat{S}}{\hat{U}}.[/math]
Добавим, что [math]\dot{S} = P + j Q.[/math] (12)
Подставляем (11) в выражение (10), получаем следующее:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N} \underline{Y}_{i k} \dot{U}_{k} = \frac{\hat{S}_i}{\hat{U}_i}, i = 1 \ldots (N-1)\end{cases}.[/math]
Подставляем (1), (3), (12) в (13), получаем:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N} \left( g_{i k} + j b_{i k} \right) \left( U_{k}' + j U_{k}'' \right) = \frac{ P_i - j Q_i }{ U_i' - j U_i'' }, i = 1 \ldots (N-1)\end{cases}.[/math]
Раскрываем скобки, домножаем правую часть на сопряженное и группируем относительно [math]j[/math]:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N} \left( g_{i k} U_k' - b_{i k} U_k'' + j \left( g_{i k} U_k'' + b_{i k} U_k' \right) \right) = \frac{P_i U_i' + Q_i U_i'' + j \left( P_i U_i'' - Q_i U_i'\right)}{U_i'^2 + U_i''^2}, i=1 \ldots (N-1)\end{cases}.[/math]
Вынесем [math]j[/math] за знак суммы в левой части, а в правой части разобьем дробное выражение на две составляющие относительно [math]j[/math], получим:
- [math]\displaystyle \begin{cases}\sum_{k=1}^{N}\left(g_{ik}U_k'-b_{ik}U_k''\right)+j\sum_{k=1}^{N}\left(g_{ik}U_k''+b_{ik}U_k'\right)=\frac{P_iU_i'+Q_iU_i''}{U_i'^2+U_i''^2}+j\frac{P_iU_i''-Q_iU_i'}{U_i'^2+U_i''^2}, i=1 \ldots (N-1)\end{cases}.[/math]
Преобразуем систему (14) к виду, аналогичному системе (8), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса токов:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N}\left(g_{ik}U_k'-b_{ik}U_k''\right)=\frac{P_iU_i'+Q_iU_i''}{U_i'^2+U_i''^2} \\ \sum_{k=1}^{N}\left(g_{ik}U_k''+b_{ik}U_k'\right)=\frac{P_iU_i''-Q_iU_i'}{U_i'^2+U_i''^2} \end{cases}, i=1 \ldots (N-1)[/math] форма баланса токов.
Выведем систему нелинейных УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей. Для этого домножим систему (13) на [math]\hat{U}[/math], получаем:
- [math]\displaystyle \begin{cases}\hat{U}_i\sum_{k=1}^{N}\underline{Y}_{ik}\dot{U}_{k}=\hat{S}_i, i=1 \ldots (N-1)\end{cases}.[/math]
Подставляем (1), (3), (12) в (16):
- [math]\displaystyle \begin{cases}\left(U_i'-jU_i''\right)\sum_{k=1}^{N}\left(g_{ik}+jb_{ik}\right)\left(U_{k}'+jU_{k}''\right)=P_i-jQ_i\end{cases}, i=1 \ldots (N-1).[/math]
Вносим сопряженный комплекс напряжения под знак суммы и группируем относительно [math]j[/math], имеем:
- [math]\displaystyle \begin{cases}\sum_{k=1}^{N}\left(\left(g_{ik}U_k'U_i'-b_{ik}U_k''U_i'+g_{ik}U_k''U_i''+b_{ik}U_k'U_i''\right)+j\left(g_{ik}U_k''U_i'+b_{ik}U_k'U_i'-g_{ik}U_k'U_i''+b_{ik}U_k''U_i''\right)\right)=P_i-jQ_i\end{cases}, i=1 \ldots (N-1).[/math]
Преобразуем систему (17) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей:
- [math]\displaystyle \begin{cases} \sum_{k=1}^{N}\left(g_{ik}\left(U_k'U_i'+U_k''U_i''\right)-b_{ik}\left(U_k''U_i'-U_k'U_i''\right)\right)=P_i \\ \sum_{k=1}^{N}\left(b_{ik}\left(U_k'U_i'+U_k''U_i''\right)+g_{ik}\left(U_k''U_i'-U_k'U_i''\right)\right)=-Q_i \end{cases}, i=1 \ldots (N-1)[/math]. форма баланса мощностей.
В полярной системе координат
Комплексное число можно представить в алгебраической, показательной и тригонометрической формах:
- [math]\displaystyle \dot{U_k}=U_k'+jU_k'' = V_k \cdot e^{jδ_k} = V_k \big(\cos(δ_k)+j \sin(δ_k)\big).[/math]
Для того, чтобы вывести УУН в форме баланса мощностей в полярной системе координат, необходимо в систему (16) подставить показательную запись комплексного числа [math]\dot{U_k}[/math]. Выполнив это, получим:
- [math]\displaystyle \begin{cases} V_i e^{-j δ_i} \sum_{k=1} \limits^{N} (g_{i \dot k} + j b_{i \dot k}) \cdot V_k \cdot e^{j δ_k} = P_i - j Q_i \end{cases}, i= \overline{ 1 \ldots (N-1) }.[/math]
Переносим экспоненты в одну сторону:
- [math]\displaystyle \begin{cases} V_i\sum_{k=1}\limits^{N}V_k(g_{ik}+jb_{ik}) \cdot e^{jδ_k} \cdot e^{-jδ_i}=P_i-jQ_i\end{cases}, i= \overline{ 1 \ldots (N-1) }.[/math]
Используя свойство степеней, выполним преобразования:
- [math]\displaystyle \begin{cases} V_i\sum_{k=1}\limits^{N} V_k (g_{ik}+jb_{ik}) \cdot e^{j(δ_k-δ_i)} = P_i - jQ_i\end{cases}, i= \overline{ 1 \ldots (N-1) }.[/math]
Переходим к тригонометрической форме:
- [math]\displaystyle \begin{cases} V_i\sum_{k=1}\limits^{N} V_k \bigg( \big(g_{ik} + jb_{ik} \big) \big( \cos(δ_k-δ_i) + j \cdot \sin(δ_k-δ_i) \big) \bigg) = P_i-jQ_i \end{cases}, i= \overline{ 1 \ldots (N-1) }.[/math]
Группируем относительно [math]j[/math]:
- [math]\displaystyle \begin{cases} V_i\sum_{k=1}\limits^{N}V_k \bigg( \big(g_{ik} \cdot \cos(δ_k-δ_i) - b_{ik} \cdot \sin(δ_k-δ_i) \big) + j \big(g_{ik} \cdot \sin(δ_k-δ_i) + b_{ik} \cdot \cos(δ_k-δ_i) \big) \bigg) = P_i - jQ_i \end{cases}, i= \overline{ 1 \ldots (N-1) }.[/math]
Преобразуем систему (19) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в полярных координатах в форме баланса мощностей:
- [math]\displaystyle \begin{cases} V_i\sum_{k=1}\limits^{N}V_k \bigg(g_{ik} \cdot \cos(δ_k-δ_i) - b_{ik} \cdot \sin(δ_k-δ_i) \bigg)=P_i \\ V_i\sum_{k=1}\limits^{N}V_k \bigg(g_{ik} \cdot \sin(δ_k-δ_i) + b_{ik} \cdot \cos(δ_k-δ_i) \bigg)=-Q_i \end{cases}, i= \overline{ 1 \ldots (N-1) }[/math] форма баланса мощностей.
Методы решения
Основные методы решения системы уравнений узловых напряжений:
- Метод Гаусса-Зейделя — это один из самых первых разработанных методов. Обычно показывает более медленную сходимость по сравнению с другими итерационными методами. Основными особенности - это малое использование памяти и не требуется матричная алгебра.
- Метод Якоби.
- Метод Z-матриц.
- Метод Ньютона-Рафсона — один из самых популярных методов решения, основанный на разложении в ряд Тейлора.
- Метод голоморфного встраивания — прямой метод расчёта на основе комплексного анализа.
Литература
- Вычислительные модели потокораспределения в электрических системах / Б. И. Аюев [и др.]; под ред. П. И. Бартоломея. — Москва : Флинта : Наука, 2008. — 254, [1] с. : ил., табл.; 22 см; ISBN 978-5-9765-0697-8.
- Powell L. Power System Load Flow Analysis. McGraw Hill Professional. — 2004.
- Wang, Xi-Fan, Song, Y.H., Irving, M. Modern power systems analysis, Springer Science, New York, 2008.
- ↑ Герасименко А.А., Федин В.Т. Передача и распределение электриче-ской энергии: Учебное пособие. – Ростов-н/Д.: Феникс; Красноярск: Издатель-ские проекты, 2006. - 720 с. (Серия «Высшее образование»)
- ↑ Идельчик В.И. Электрические системы и сети: Учебник для вузов. - М.: Энергоатомиздат, 1989. - 592 с.
- ↑ Электрические системы. Электрические сети/Под ред. В.А. Веникова и В.А. Строева - М.: Высш. шк., 1998, 512 с.
- ↑ Электрические системы. Передача энергии переменным и постоянным током высокого напряжения / Под ред. В.А. Веникова. - М.: Высш. шк., 1971, Т. 3, 368 с.