Ручной расчёт установившегося режима сети с двухсторонним питанием — различия между версиями
Windsl (обсуждение | вклад) м (→Расчет потокораспределения без учета потерь мощности методом контурных уравнений) |
Agro (обсуждение | вклад) (→Обратный ход по напряжениям) |
||
| Строка 234: | Строка 234: | ||
: <math>\displaystyle \Delta \dot{U}_{B3} = \frac{P_{B3н}\cdot R_{B-3}+Q_{B3н}\cdot X_{B-3}}{|\dot U_{B}|} = \frac{-4,548\cdot 2,4+(-9,535)\cdot 8,1}{110} = -0,801</math> кВ; | : <math>\displaystyle \Delta \dot{U}_{B3} = \frac{P_{B3н}\cdot R_{B-3}+Q_{B3н}\cdot X_{B-3}}{|\dot U_{B}|} = \frac{-4,548\cdot 2,4+(-9,535)\cdot 8,1}{110} = -0,801</math> кВ; | ||
| − | : <math>\displaystyle \delta \dot{U}_{ | + | : <math>\displaystyle \delta \dot{U}_{B3} = \frac{P_{B3н}\cdot X_{B-3}-Q_{B3н}\cdot R_{B-3}}{|\dot U_{B}|} = \frac{-4,548\cdot 8,1-(-9,535)\cdot 2,4}{110} = -0,127</math> кВ; |
: <math>\displaystyle \dot U_{3}=|\dot U_{B}|-\Delta U_{B3} - j\delta U_{B3}=110-(-0,801)-(-j0,127)=110,801\angle 0,066^\circ</math> кВ; | : <math>\displaystyle \dot U_{3}=|\dot U_{B}|-\Delta U_{B3} - j\delta U_{B3}=110-(-0,801)-(-j0,127)=110,801\angle 0,066^\circ</math> кВ; | ||
: <math>\displaystyle {\phi}_{3}=\angle 0,066^\circ-\angle 2^\circ=\angle -1,934^\circ</math>; | : <math>\displaystyle {\phi}_{3}=\angle 0,066^\circ-\angle 2^\circ=\angle -1,934^\circ</math>; | ||
| Строка 267: | Строка 267: | ||
: <math>\displaystyle \dot U_{4′}=|\dot U_{1′′}|-\Delta U_{1′′4′}-j\delta U_{1′′4′}=111,912-1,249-j1,318=110,671\angle -0,682^\circ</math> кВ; | : <math>\displaystyle \dot U_{4′}=|\dot U_{1′′}|-\Delta U_{1′′4′}-j\delta U_{1′′4′}=111,912-1,249-j1,318=110,671\angle -0,682^\circ</math> кВ; | ||
: <math>\displaystyle {\phi}_{4′}=\angle -0,682^\circ-\angle 2^\circ=\angle -2,682^\circ</math>. | : <math>\displaystyle {\phi}_{4′}=\angle -0,682^\circ-\angle 2^\circ=\angle -2,682^\circ</math>. | ||
| − | |||
==== Расчет уравнительных перетоков мощности ==== | ==== Расчет уравнительных перетоков мощности ==== | ||
Версия 13:17, 24 июня 2020
В статье приведено описание метода ручного расчёта сложно-замкнутой электрической сети с двухсторонним питанием.
Содержание
- 1 Теоретические основы
- 2 Пример расчёта сложно-замкнутой электрической сети с двухсторонним питанием
- 2.1 Задание
- 2.2 Исходные данные
- 2.3 Решение
- 2.4 Файлы для скачивания
Теоретические основы
Алгоритм расчёта сети с двухсторонним питанием:
- Составление схемы замещения.
- Выбор условно-положительного направления мощностей.
- Приравнивание напряжений базисных узлов.
- Расчет сети без учета потерь мощности.
- Расчет уравнительного перетока между базисными узлами.
- Наложение уравнительного перетока на результаты расчета п. 4.
- Нахождение точек потокораздела (при необходимости).
- Расчет полученной разветвленной сети с потерями мощности.
- Расчёт уравнительных перетоков в узлах потокораздела.
- Уточнить мощности шунтов, в соответствие с новыми уровнями напряжений.
- Повторять с пункта 8 до достижения критерия остановки итерационного процесса.
Пример расчёта сложно-замкнутой электрической сети с двухсторонним питанием
Задание
Основные задачи расчёта:
- Выполнить расчёт распределения потоков мощностей с учётом потерь мощности.
Исходные данные
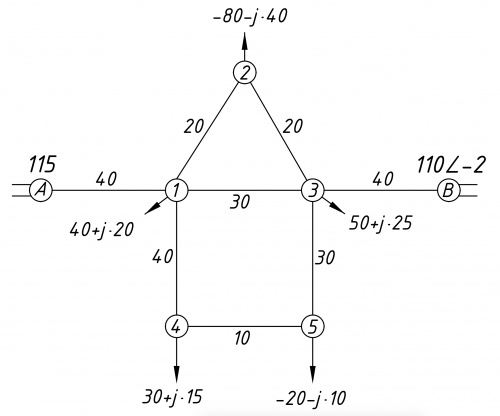
- Исходная схема электрической сети представлена на рисунке 1.
- Мощности нагрузок узлов:
- [math]\displaystyle \dot S_{1}=40+j20 \text{ МВА }; [/math]
- [math]\displaystyle \dot S_{2}=-80-j40 \text{ МВА }; [/math]
- [math]\displaystyle \dot S_{3}=50+j25 \text{ МВА }; [/math]
- [math]\displaystyle \dot S_{4}=30+j15 \text{ МВА }; [/math]
- [math]\displaystyle \dot S_{5}=-20-j10 \text{ МВА }; [/math]
- Напряжения базисных узлов:[math]\displaystyle \dot{U}_{\text{А}} = 115 \angle 0^\circ [/math] кВ, [math]\displaystyle \dot{U}_{\text{B}}=110 \angle - 2^\circ [/math] кВ.
- Марка проводов ЛЭП:
- A-1: АС-240, 40 км;
- B-3: АС-240, 20 км;
- 1-2: АС-240, 20 км;
- 1-3: АС-240, 30 км;
- 1-4: АС-240, 40 км;
- 2-3: АС-240, 20 км;
- 3-5: АС-240, 30 км;
- 4-5: АС-240, 10 км.
Решение
Расчет параметров схемы замещения
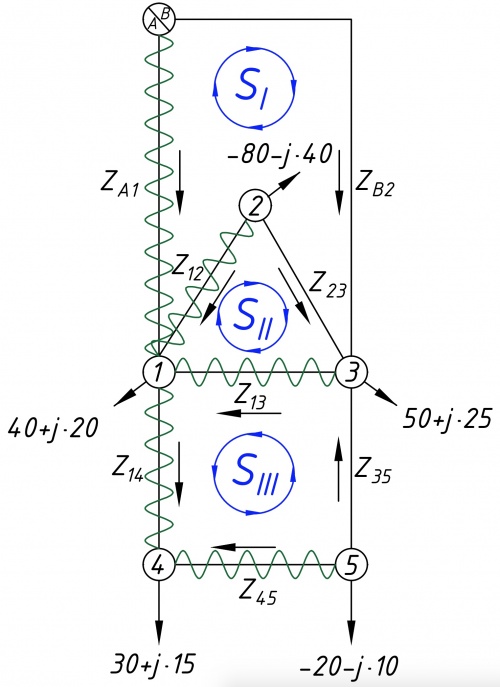
Схема замещения сети и её параметров, приведена на рисунке 2. Расчет параметров для ЛЭП выполнен на основе справочных данных параметров ЛЭП
ЛЭП A-1:
- [math]\displaystyle \underline Z_{A-1}=\frac {R_{0} \cdot L_{A-1}}{100}+\frac {X_{0} \cdot L_{A-1}}{100} = \frac {0,12 \cdot 40}{100}+\frac {0,405 \cdot 40}{100} = 4,8+j16,2 [/math] Ом;
- [math]\displaystyle \underline Y_{A-1}= j \frac {B_{0} \cdot L_{A-1}}{100} = j \frac {2,81 \cdot 40}{100}= j112,4 [/math] мкСм.
ЛЭП B-3:
- [math]\displaystyle \underline Z_{B-3}=\frac {R_{0} \cdot L_{B-3}}{100}+\frac {X_{0} \cdot L_{B-3}}{100} = \frac {0,12 \cdot 20}{100}+\frac {0,405 \cdot 20}{100} = 2,4+j8,1 [/math] Ом;
- [math]\displaystyle \underline Y_{B-3}= j \frac {B_{0} \cdot L_{B-3}}{100} = j \frac {2,81 \cdot 20}{100}= j56,2 [/math] мкСм.
ЛЭП 1-2:
- [math]\displaystyle \underline Z_{1-2}=\frac {R_{0} \cdot L_{1-2}}{100}+\frac {X_{0} \cdot L_{1-2}}{100} = \frac {0,12 \cdot 20}{100}+\frac {0,405 \cdot 20}{100} = 2,4+j8,1 [/math] Ом;
- [math]\displaystyle \underline Y_{1-2}= j \frac {B_{0} \cdot L_{1-2}}{100} = j \frac {2,81 \cdot 20}{100}= j56,2 [/math] мкСм.
ЛЭП 1-3:
- [math]\displaystyle \underline Z_{1-3}=\frac {R_{0} \cdot L_{1-3}}{100}+\frac {X_{0} \cdot L_{1-3}}{100} = \frac {0,12 \cdot 30}{100}+\frac {0,405 \cdot 30}{100} = 3,6+j12,15 [/math] Ом;
- [math]\displaystyle \underline Y_{1-3}= j \frac {B_{0} \cdot L_{1-3}}{100} = j \frac {2,81 \cdot 30}{100}= j84,3 [/math] мкСм.
ЛЭП 1-4:
- [math]\displaystyle \underline Z_{1-4}=\frac {R_{0} \cdot L_{1-4}}{100}+\frac {X_{0} \cdot L_{1-4}}{100} = \frac {0,12 \cdot 40}{100}+\frac {0,405 \cdot 40}{100} = 4,8+j16,2 [/math] Ом;
- [math]\displaystyle \underline Y_{1-4}= j \frac {B_{0} \cdot L_{1-4}}{100} = j \frac {2,81 \cdot 40}{100}= j112,4 [/math] мкСм.
ЛЭП 2-3:
- [math]\displaystyle \underline Z_{2-3}=\frac {R_{0} \cdot L_{2-3}}{100}+\frac {X_{0} \cdot L_{2-3}}{100} = \frac {0,12 \cdot 20}{100}+\frac {0,405 \cdot 20}{100} = 2,4+j8,1 [/math] Ом;
- [math]\displaystyle \underline Y_{2-3}= j \frac {B_{0} \cdot L_{2-3}}{100} = j \frac {2,81 \cdot 20}{100}= j56,2 [/math] мкСм.
ЛЭП 3-5:
- [math]\displaystyle \underline Z_{3-5}=\frac {R_{0} \cdot L_{3-5}}{100}+\frac {X_{0} \cdot L_{3-5}}{100} = \frac {0,12 \cdot 30}{100}+\frac {0,405 \cdot 30}{100} = 3,6+j12,15 [/math] Ом;
- [math]\displaystyle \underline Y_{3-5}= j \frac {B_{0} \cdot L_{3-5}}{100} = j \frac {2,81 \cdot 30}{100}= j84,3 [/math] мкСм.
ЛЭП 4-5:
- [math]\displaystyle \underline Z_{4-5}=\frac {R_{0} \cdot L_{4-5}}{100}+\frac {X_{0} \cdot L_{4-5}}{100} = \frac {0,12 \cdot 10}{100}+\frac {0,405 \cdot 10}{100} = 1,2+j4,05 [/math] Ом;
- [math]\displaystyle \underline Y_{4-5}= j \frac {B_{0} \cdot L_{4-5}}{100} = j \frac {2,81 \cdot 10}{100}= j28,1 [/math] мкСм.
Расчет потокораспределения без учета потерь мощности методом контурных уравнений
Приравняем напряжения базисных узлов и получим схему, предствленную на рисунке 3.
Синим цветом выделены контурные потоки мощности. Зеленым цветом веделено дерево графа схемы. Контур I — A1,13,B3; контур II — 12, 23, 13; контур III — 13, 35, 45, 14.
Контурные (хордовые) перетоки мощности:
- [math] \left\{ \begin{matrix} \dot S_{B-3} = \dot S_{I}\\ \dot S_{2-3} = \dot S_{II} \\ \dot S_{3-5} = \dot S_{III} \end{matrix} \right. [/math]
Собственные сопротивления контуров:
- [math]\displaystyle \underline Z_{I-I} = \underline Z_{A-1} + \underline Z_{B-3} + \underline Z_{1-3} = 4,8 + j16,2 + 2,4 + j8,1 + 3,6 + j12,15 = 10,8 + j36,45[/math] Ом;
- [math]\displaystyle \underline Z_{II-II} = \underline Z_{1-2} + \underline Z_{2-3} + \underline Z_{1-3} = 2,4 + j8,1 + 2,4 + j8,1 + 3,6 + j12,15 = 8,4 + j28,35[/math] Ом;
- [math]\displaystyle \underline Z_{III-III} = \underline Z_{1-3} + \underline Z_{1-4} + \underline Z_{4-5}+\underline Z_{3-5} = 3,6 + j12,15 + 4,8 + j16,2 + 1,2 + j4,05 + 3,6 + j12,15 = 13,2 + j44,55[/math] Ом.
Смежные сопротивления контуров:
- Так как все контура между собой соприкасаются по ветви 13, то:
- [math]\displaystyle \underline Z_{I-II}=\underline Z_{II-I}=\underline Z_{I-III}=\underline Z_{III-I}=\underline Z_{II-III}=\underline Z_{III-II}=\underline Z_{1-3}=3,6+j12,15[/math] Ом.
Свободные слагаемые:
- [math]\displaystyle С_{I}=- \dot S_{1}\cdot\hat Z_{A-1}-\dot S_{2}\cdot\hat Z_{A-1}-\dot S_{3}\cdot(\hat Z_{A-1}+ \hat Z_{1-3})-\dot S_{4}\cdot\hat Z_{A-1}-\dot S_{5}\cdot\hat Z_{A-1}[/math];
- [math]\displaystyle С_{I}=-(40+j20)\cdot(4,8-16,2)-(-80-j40)\cdot(4,8-j16,2)-(50+j25)\cdot(4,8-j16,2+3,6-j12,15)-(30+j15)\cdot(4,8-j16,2)-(-20-j10)\cdot(4,8-j16,2)[/math];
- [math]\displaystyle С_{I}=-741,75+j793,5[/math];
- [math]\displaystyle С_{II}=\dot S_{2}\cdot\hat Z_{1-2}-\dot S_{3}\cdot\hat Z_{1-3}=(-80-j40)\cdot(2,4-8,1)-(50+j25)\cdot(3,6-j12,15)=-999,75+j1069,5[/math];
- [math]\displaystyle С_{III}=-\dot S_{3}\cdot\hat Z_{1-3}+\dot S_{4}\cdot\hat Z_{1-4}+\dot S_{5}\cdot(\hat Z_{1-4}+\hat Z_{4-5})=-(50+j25)\cdot(3,6-12,15)+(30+j15)\cdot(4,8-j16,2)+(-20-j10)\cdot(4,8-j16,2+1,2-j4,05)[/math];
- [math]\displaystyle С_{III}=-419,25+j448,5[/math].
Контурные уравнения:
- [math]\displaystyle \left\{ \begin{matrix} \dot S_{I}\cdot\hat Z_{I-I}+\dot S_{II}\cdot\hat Z_{I-II}+\dot S_{III}\cdot\hat Z_{I-III}+ С_{I}=0\\ \dot S_{I}\cdot\hat Z_{II-I}+\dot S_{II}\cdot\hat Z_{II-II}+\dot S_{III}\cdot\hat Z_{II-III}+ С_{II}=0 \\ \dot S_{I}\cdot\hat Z_{III-I}+\dot S_{II}\cdot\hat Z_{III-II}+\dot S_{III}\cdot\hat Z_{III-III}+ С_{III}=0 \end{matrix} \right. [/math]
Решив данную СЛАУ [1] имеем:
- [math]\displaystyle \left\{ \begin{matrix} \dot S_{I}=13,175+j6,587 \text{ МВА }\\ \dot S_{II}=39,762+19,881 \text{ МВА } \\ \dot S_{III}=-2,619-j1,31 \text{ МВА } \end{matrix} \right. [/math]
Перетоки мощности в остальных ветвях:
- [math]\displaystyle \dot S_{1-3}=-\dot S_{3}+\dot S_{I}+\dot S_{II}+\dot S_{III}=-(50+j25)+13,175+j6,587+39,762+j19,881+(-2,619-j1,31)=0,317+j0,159 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{4-5}=-\dot S_{5}-\dot S_{III}=-(-20-j10)-(-2,619-j1,31)=22,619+j11,31 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1-4}=-\dot S_{4-5}+\dot S_{4}=-(22,619+j11,31)+30+j15=7,381+j3,69 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1-2}=-\dot S_{II}-\dot S_{2}=-(39,762+j19,881)-(-80-j40)=40,238+j20,119 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{A-1}=\dot S_{1}+\dot S_{1-4}-\dot S_{1-2}-\dot S_{1-3}=40+j20+7,381+j3,69-(40,238+j20,119)-(0,317+j0,159)=6,825+j3,413 \text{ МВА }[/math].
Расчет уравнительного перетока мощности между базами
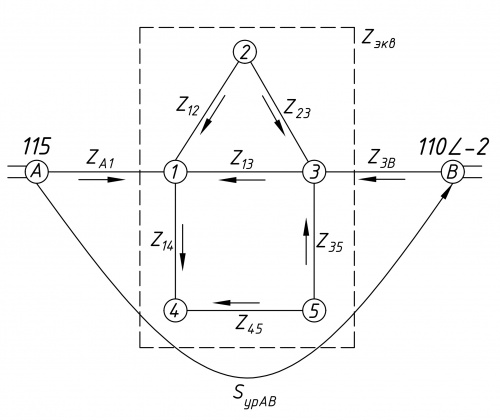
Схема с уравнительным перетоком мощности изображена на рисунке 4.
Эквивалентные сопротивления:
- [math] \displaystyle\underline Z_{ЭКВ}=\frac{\underline Z_{1-3}\cdot(\underline Z_{1-2}+\underline Z_{2-3})\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})}{\underline Z_{1-3}\cdot(\underline Z_{1-2}+\underline Z_{2-3})+\underline Z_{1-3}\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})+(\underline Z_{1-2}+\underline Z_{2-3})\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})}[/math];
- [math] \displaystyle \underline Z_{1-2}+\underline Z_{2-3}=2,4+j8,1+2,4+j8,1=4,8+j16,2\text{ Ом }[/math];
- [math] \displaystyle \underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5}=4,8+j16,2+1,2+j4,05+3,6+j12,15=9,6+j32,4\text{ Ом }[/math];
- [math] \displaystyle\underline Z_{ЭКВ}=\frac{(3,6+j12,15)\cdot(4,8+j16,2)\cdot(9,6+j32,4)}{(3,6+j12,15)\cdot(4,8+j16,2)+(3,6+j12,15)\cdot(9,6+j32,4)+(4,8+j16,2)\cdot(9,6+j32,4)}=1,694+j5,718\text{ Ом }[/math];
- [math] \displaystyle\underline Z_{A-B}=\underline Z_{A-1}+\underline Z_{ЭКВ}+\underline Z_{B-3}=4,8+j16,2+1,694+j5,718+2,4+j8,1=8,894+j30,018\text{ Ом }[/math].
Уравнительный переток:
- [math]\displaystyle \dot S_{урA-B}= \frac{\dot U_{A}+\dot U_{B}}{2}\cdot \frac{\hat{\dot U_{A}}-\hat{\dot U_{B}}}{\hat Z_{A-B}}=\frac{115 \angle 0^\circ + 110 \angle - 2^\circ}{2}\cdot \frac{115 \angle 0^\circ -110 \angle - 2^\circ}{8,894-j30,018}=18,625+j13,221\text{ МВА }[/math].
Уравнительный переток распределяется по ветвям пропорционально сопротивлениям:
- [math]\displaystyle \dot S_{ур1-3}= \dot S_{урA-B}\cdot\frac{\hat Z_{ЭКВ}}{\hat Z_{1-3}}=(18,625+j13,221)\cdot\frac{1,694-j5,718}{3,6-j12,15}=8,764+j6,221\text{ МВА }[/math];
- [math]\displaystyle \dot S_{ур1-2-3}= \dot S_{урA-B}\cdot\frac{\hat Z_{ЭКВ}}{\hat Z_{1-2}+\hat Z_{2-3}}=(18,625+j13,221)\cdot\frac{1,694-j5,718}{4,8-j16,2}=6,573+j4,666\text{ МВА }[/math];
- [math]\displaystyle \dot S_{ур1-4-5-3}= \dot S_{урA-B}\cdot\frac{\hat Z_{ЭКВ}}{\hat Z_{1-4}+\hat Z_{4-5}+\hat Z_{3-5}}=(18,625+j13,221)\cdot\frac{1,694-j5,718}{9,6-j32,4}=3,287+j2,333\text{ МВА }[/math].
Перетоки мощности в ветвях с учетом уравнительного перетока:
- [math]\displaystyle \dot S_{A-1}=\dot S_{A-1}+\dot S_{урA-B}=6,825+j3,413+18,625+j13,221=25,45+j16,633 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{B-3}=\dot S_{B-3}-\dot S_{урA-B}=13,175+j6,587-(18,625+j13,221)=-5,45-j6,633 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1-2}=\dot S_{1-2}-\dot S_{ур1-2-3}=40,238+j20,119-(6,573+j4,666)=33,665+j15,453 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1-3}=\dot S_{1-3}-\dot S_{ур1-3}=0,317+j0,159-(8,764+j6,221)=-8,447-j6,063 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1-4}=\dot S_{1-4}+\dot S_{ур1-4-5-3}=7,381+j3,69+3,287+j2,333=10,668+j6,024 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{2-3}=\dot S_{2-3}+\dot S_{ур1-2-3}=39,762+j19,881+6,573+j4,666=46,335+j24,547 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{3-5}=\dot S_{3-5}+\dot S_{ур1-4-5-3}=-2,619-j1,31+3,287+j2,333=0,668+j1,024 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{4-5}=\dot S_{4-5}-\dot S_{ур1-4-5-3}=22,619+j11,31-(3,287+j2,333)=19,332+j8,976 \text{ МВА }[/math].
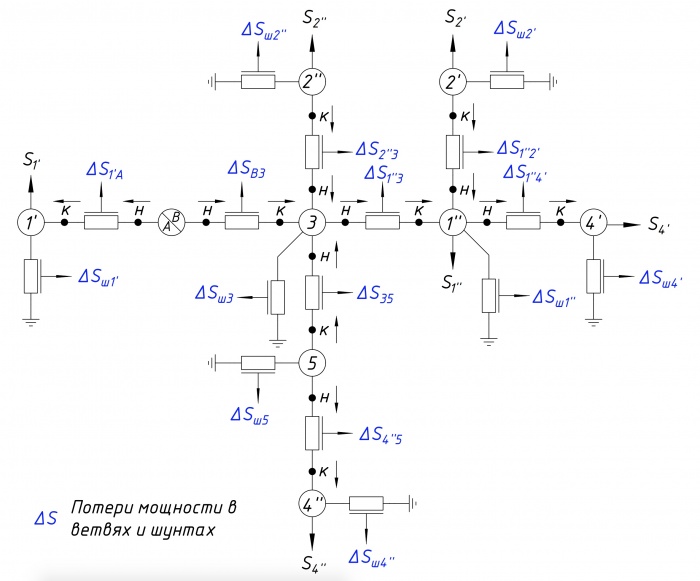
Расчет разветвленной сети с учетом потерь мощности
Пусть точки потокораздела — узлы 1, 2, 4. Расчетная схема представлена на рисунке 5.
Начальные приближения
- [math]\displaystyle \dot{U_{1′}}=110 \angle - 2^\circ [/math] кВ;
- [math]\displaystyle \dot{U_{1′′}}=115 \angle 0^\circ[/math] кВ;
- [math]\displaystyle \dot{U_{2′}}=115 \angle 0^\circ[/math] кВ;
- [math]\displaystyle \dot{U_{2′′}}=115 \angle 0^\circ[/math] кВ;
- [math]\displaystyle \dot{U_{3}}=115 \angle 0^\circ[/math] кВ;
- [math]\displaystyle \dot{U_{4′}}=115 \angle 0^\circ[/math] кВ;
- [math]\displaystyle \dot{U_{4′′}}=115 \angle 0^\circ[/math] кВ;
- [math]\displaystyle \dot{U_{5}}=115 \angle 0^\circ[/math] кВ.
Расчет потерь мощности в шунтах
- [math]\displaystyle \dot{ΔS_{ш1′}}=\dot {|U_{1′}|}^{2}\cdot \frac {\hat Y_{A-1}}{2}={110}^{2}\cdot \frac {-j112,4}{2}\cdot 10^{-6}=-j0,68 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш1′′}}=\dot {|U_{1′′}|}^{2}\cdot \left( \frac {\hat Y_{1-2}}{2}+\frac {\hat Y_{1-3}}{2}+\frac {\hat Y_{1-4}}{2} \right)={115}^{2}\cdot \left( \frac {-j56,2}{2}+\frac {-j84,3}{2}+\frac {-j112,4}{2}\right)\cdot 10^{-6}=-j1,672 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш2′}}=\dot {|U_{2′}|}^{2}\cdot \frac {\hat Y_{1-2}}{2}={115}^{2}\cdot \frac {-j56,2}{2}\cdot 10^{-6}=-j0,372 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш2′′}}=\dot {|U_{2′′}|}^{2}\cdot \frac {\hat Y_{2-3}}{2}={115}^{2}\cdot \frac {-j56,2}{2}\cdot 10^{-6}=-j0,372 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш3}}=\dot {|U_{3}|}^{2}\cdot\left( \frac {\hat Y_{1-3}}{2}+\frac {\hat Y_{B-3}}{2}+\frac {\hat Y_{3-5}}{2}\frac {\hat Y_{2-3}}{2}\right)={115}^{2}\cdot \left( \frac {-j84,3}{2}+\frac {-j56,2}{2}+\frac {-j84,3}{2}+\frac {-j56,2}{2}\right)\cdot 10^{-6}=-j1,858 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш4′}}=\dot {|U_{4′}|}^{2}\cdot \frac {\hat Y_{1-4}}{2}={115}^{2}\cdot \frac {-j112,4}{2}\cdot 10^{-6}=-j0,743 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш4′′}}=\dot {|U_{4′′}|}^{2}\cdot \frac {\hat Y_{4-5}}{2}={115}^{2}\cdot \frac {-j28,1}{2}\cdot 10^{-6}=-j0,186 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш5}}=\dot {|U_{5}|}^{2}\cdot\left( \frac {\hat Y_{4-5}}{2}+\frac {\hat Y_{3-5}}{2}\right)={115}^{2}\cdot \left( \frac {-j28,1}{2}+\frac {-j84,3}{2}\right)\cdot 10^{-6}=-j0,743 \text{ МВА } [/math].
Расчет узловых мощностей
- [math]\displaystyle \dot S_{1′}=\dot S_{A-1}=25,45+j16,633 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1′′}=\dot S_{1-2}+\dot S_{1-3}-\dot S_{1-4}=33,665+j15,453+(-8,447-j6,063)-(10,668+j6,024)=14,55+j3,367 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{2′}=-\dot S_{1-2}=-33,665-j15,453 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{2′′}=-\dot S_{2-3}=-46,335-j24,547 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{3}=50+j25 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{4′}=\dot S_{1-4}=10,668+j6,024 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{4′′}=\dot S_{4-5}=19,332+j8,976 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{5}=-20-j10 \text{ МВА }[/math].
Прямой ход по мощностям
- [math]\displaystyle \dot {S}_{1′Aк}=\dot{S}_{1′}+\Delta \dot S_{ш1′} = 25,45+j16,633+(-j0,68)=25,45+j15,953 \text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{1′A} = \frac{P_{1′Aк}^{2}+Q_{1′Aк}^{2}}{|\dot U_{1′}|^{2}}\cdot \underline{Z}_{A-1} = \frac{25,45^{2}+15,953^{2}}{110^{2}}\cdot (4,8+j16,2) = 0,358+j1,208\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′Aн}=\dot{S}_{1′Aк}+\Delta \dot{S}_{1′A}=25,45+j15,953+0,358+j1,208=25,808+j17,161 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′′4′к}=\dot{S}_{4′}+\Delta \dot S_{ш4′} = 10,668+j6,024+(-j0,743)=10,668+j5,28 \text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{1′′4′} = \frac{P_{1′′4′к}^{2}+Q_{1′′4′к}^{2}}{|\dot U_{4′}|^{2}}\cdot \underline{Z}_{1-4} = \frac{10,668^{2}+5,28^{2}}{115^{2}}\cdot (4,8+j16,2) = 0,051+j0,174 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′′4′н}=\dot{S}_{1′′4′к}+\Delta \dot{S}_{1′′4′}=10,668+j5,28+0,051+j0,174=10,719+j5,454\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′′2′к}=-\dot{S}_{2′}-\Delta \dot S_{ш2′} =-(-33,665-j15,453)-(-j0,372)=33,665+j15,825\text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{1′′2′} = \frac{P_{1′′2′к}^{2}+Q_{1′′2′к}^{2}}{|\dot U_{2′}|^{2}}\cdot \underline{Z}_{1-2} = \frac{33,665^{2}+15,825^{2}}{115^{2}}\cdot (2,4+j8,1) = 0,251+j0,848 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′′2′н}=\dot{S}_{1′′2′к}-\Delta \dot S_{1′′2′}=33,665+j15,825-(0,251+j0,848)=33,414+j14,977\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′′3к}=\dot{S}_{1′′}+\dot{S}_{1′′4′н}-\dot {S}_{1′′2′н}+\Delta \dot S_{ш1′′}=14,55+j3,367+10,719+j5,454-(33,414+j14,977)+(-j1,672)=-8,144-j7,829\text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{1′′3} = \frac{P_{1′′3к}^{2}+Q_{1′′3к}^{2}}{|\dot U_{1′′}|^{2}}\cdot \underline{Z}_{1-3} = \frac{(-8,144)^{2}+(-j7,829)^{2}}{115^{2}}\cdot (3,6+j12,15) = 0,035+j0,117 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{1′′3н}=\dot{S}_{1′′3к}+\Delta \dot S_{1′′3}=-8,144-j7,829+0,035+j0,117=-8,11-j7,712\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{2′′3к}=-\dot{S}_{2′′}-\Delta \dot S_{ш2′′}=-(-46,335-j24,547)-(-j0,372)=46,335+j24,919\text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{2′′3} = \frac{P_{2′′3к}^{2}+Q_{2′′3к}^{2}}{|\dot U_{2′′}|^{2}}\cdot \underline{Z}_{2-3} = \frac{46,335^{2}+24,919^{2}}{115^{2}}\cdot (2,4+j8,1) = 0,502+j1,695 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{2′′3н}=\dot{S}_{2′′3к}-\Delta \dot S_{2′′3}=46,335+j24,919-(0,502+j1,695)=45,833+j23,223\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{4′′5к}=\dot{S}_{4′′}+\Delta \dot S_{ш4′′}=19,332+j8,976+(-j0,186)=19,332+j8,791\text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{4′′5} = \frac{P_{4′′5к}^{2}+Q_{4′′5к}^{2}}{|\dot U_{4′′}|^{2}}\cdot \underline{Z}_{4-5} = \frac{19,332^{2}+8,791^{2}}{115^{2}}\cdot (1,2+j4,05) = 0,041+j0,138 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{4′′5н}=\dot{S}_{4′′5к}+\Delta \dot S_{4′′5}=19,332+j8,791+0,041+j0,138=19,373+j8,929\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{35к}=-\dot{S}_{4′′5н}-\dot{S}_{5}-\Delta \dot S_{ш5}=-(19,373+j8,929)-(-20-j10)-(-j0,743)=0,627+j1,814\text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{35} = \frac{P_{35к}^{2}+Q_{35к}^{2}}{|\dot U_{5}|^{2}}\cdot \underline{Z}_{3-5} = \frac{0,627^{2}+1,814^{2}}{115^{2}}\cdot (3,6+j12,15) = 1,003\cdot 10^{-3}+3,385i\cdot 10^{-3} \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{35н}=\dot{S}_{35к}-\dot{S}_{35}=0,627+j1,814-(1,003\cdot 10^{-3}+3,385i\cdot 10^{-3})=0,626+j1,811\text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{B3к}=-\dot{S}_{1′′3н}-\dot{S}_{35н}-\dot{S}_{2′′3н}+\dot{S}_{3}+\Delta \dot S_{ш3}=-8,11-j7,712-(0,626+j1,811)-(45,833+j23,223)+50+j25+(-j1,858)=-4,568-j9,604\text{ МВА }[/math];
- [math]\displaystyle \Delta \dot{S}_{B3} = \frac{P_{B3к}^{2}+Q_{B3к}^{2}}{|\dot U_{3}|^{2}}\cdot \underline{Z}_{B-3} = \frac{(-4,568)^{2}+(-9,604)^{2}}{115^{2}}\cdot (2,4+j8,1) = 0,021+j0,069 \text{ МВА }[/math];
- [math]\displaystyle \dot {S}_{B3н}=\dot{S}_{B3к}+\Delta \dot{S}_{B3}=-4,568-j9,604+0,021+j0,069=-4,548-j9,535\text{ МВА }[/math].
Обратный ход по напряжениям
- [math]\displaystyle \Delta \dot{U}_{1′A} = \frac{P_{1′Aн}\cdot R_{A-1}+Q_{1′Aн}\cdot X_{A-1}}{|\dot U_{A}|} = \frac{25,808\cdot 4,8+17,161\cdot 16,2}{115} = 3,495[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{1′A} = \frac{P_{1′A}\cdot X_{A-1}-Q_{1′A}\cdot R_{A-1}}{|\dot U_{A}|} = \frac{25,808\cdot 16,2-17,161\cdot 4,8}{115} = 2,919[/math] кВ;
- [math]\displaystyle \dot U_{1′}=|\dot U_{A}|-\Delta U_{1′A} - j\delta U_{1′A}=115-3,495-j2,919=111,544\angle -1,5^\circ[/math] кВ;
- [math]\displaystyle \Delta \dot{U}_{B3} = \frac{P_{B3н}\cdot R_{B-3}+Q_{B3н}\cdot X_{B-3}}{|\dot U_{B}|} = \frac{-4,548\cdot 2,4+(-9,535)\cdot 8,1}{110} = -0,801[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{B3} = \frac{P_{B3н}\cdot X_{B-3}-Q_{B3н}\cdot R_{B-3}}{|\dot U_{B}|} = \frac{-4,548\cdot 8,1-(-9,535)\cdot 2,4}{110} = -0,127[/math] кВ;
- [math]\displaystyle \dot U_{3}=|\dot U_{B}|-\Delta U_{B3} - j\delta U_{B3}=110-(-0,801)-(-j0,127)=110,801\angle 0,066^\circ[/math] кВ;
- [math]\displaystyle {\phi}_{3}=\angle 0,066^\circ-\angle 2^\circ=\angle -1,934^\circ[/math];
- [math]\displaystyle \Delta \dot{U}_{2′′3} = \frac{P_{2′′3н}\cdot R_{2-3}+Q_{2′′3н}\cdot X_{2-3}}{|\dot U_{3}|} = \frac{45,833\cdot 2,4+23,223\cdot 8,1}{110,801} = 2,69[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{2′′3} = \frac{P_{2′′3н}\cdot X_{2-3}-Q_{2′′3н}\cdot R_{2-3}}{|\dot U_{3}|} = \frac{45,833\cdot 8,1-23,223\cdot 2,4}{110,801} = 2,848[/math] кВ;
- [math]\displaystyle \dot U_{2′′}=|\dot U_{3}|+\Delta U_{2′′3}+j\delta U_{2′′3}=110,801+2,69+j2,848=113,528\angle 1,437^\circ[/math] кВ;
- [math]\displaystyle {\phi}_{2′′}=\angle 1,437^\circ-\angle 2^\circ=\angle -0,563^\circ[/math];
- [math]\displaystyle \Delta \dot{U}_{35} = \frac{P_{35н}\cdot R_{3-5}+Q_{35н}\cdot X_{3-5}}{|\dot U_{3}|} = \frac{0,626\cdot 3,6+1,811\cdot 12,15}{110,801} = 0,219[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{35} = \frac{P_{35н}\cdot X_{3-5}-Q_{35н}\cdot R_{3-5}}{|\dot U_{3}|} = \frac{0,626\cdot 12,15-1,811\cdot 3,6}{110,801} = 9,769\cdot 10^{-3}[/math] кВ;
- [math]\displaystyle \dot U_{5}=|\dot U_{3}|+\Delta U_{35}+j\delta U_{35}=110,801+0,219+j9,769\cdot 10^{-3}=111,02\angle 5,042\cdot 10^{-3\circ}[/math] кВ;
- [math]\displaystyle {\phi}_{5}=\angle 5,042\cdot 10^{-3\circ}-\angle 2^\circ=\angle -1,995^\circ[/math];
- [math]\displaystyle \Delta \dot{U}_{4′′5} = \frac{P_{4′′5н}\cdot R_{4-5}+Q_{4′′5н}\cdot X_{4-5}}{|\dot U_{5}|} = \frac{19,373\cdot 1,2+8,929\cdot 4,05}{111,02} = 0,535[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{4′′5} = \frac{P_{4′′5н}\cdot X_{4-5}-Q_{4′′5н}\cdot R_{4-5}}{|\dot U_{5}|} = \frac{19,373\cdot 4,05-8,929\cdot 1,2}{111,02} = 0,61[/math] кВ;
- [math]\displaystyle \dot U_{4′′}=|\dot U_{5}|-\Delta U_{4′′5}-j\delta U_{4′′5}=111,02-0,535-j0,61=110,487\angle -0,316^\circ[/math] кВ;
- [math]\displaystyle {\phi}_{4′′}=\angle -0,316^\circ-\angle 2^\circ=\angle -2,316^\circ[/math];
- [math]\displaystyle \Delta \dot{U}_{1′′3} = \frac{P_{1′′3н}\cdot R_{1-3}+Q_{1′′3н}\cdot X_{1-3}}{|\dot U_{3}|} = \frac{-8,11\cdot 3,6+(-7,712)\cdot 12,15}{110,801} = -1,109[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{1′′3} = \frac{P_{1′′3н}\cdot X_{1-3}-Q_{1′′3н}\cdot R_{1-3}}{|\dot U_{3}|} = \frac{-8,11\cdot 12,15-(-7,712)\cdot 3,6}{110,801} = -0,639[/math] кВ;
- [math]\displaystyle \dot U_{1′′}=|\dot U_{3}|-\Delta U_{1′′3}-j\delta U_{1′′3}=110,801-(-1,109)-(-j0,639)=111,912\angle 0,327^\circ[/math] кВ;
- [math]\displaystyle {\phi}_{1′′}=\angle 0,327^\circ-\angle 2^\circ=\angle -1,673^\circ[/math];
- [math]\displaystyle \Delta \dot{U}_{1′′2′} = \frac{P_{1′′2′н}\cdot R_{1-2}+Q_{1′′2′н}\cdot X_{1-2}}{|\dot U_{1′′}|} = \frac{33,414\cdot 2,4+14,977\cdot 8,1}{111,912} = 1,801[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{1′′2′} = \frac{P_{1′′2′н}\cdot X_{1-2}-Q_{1′′2′н}\cdot R_{1-2}}{|\dot U_{1′′}|} = \frac{33,414\cdot 8,1-14,977\cdot 2,4}{111,912} = 2,097[/math] кВ;
- [math]\displaystyle \dot U_{2′}=|\dot U_{1′′}|+\Delta U_{1′′2′}+j\delta U_{1′′2′}=111,912+1,801+j2,097=113,732\angle 1,057^\circ[/math] кВ;
- [math]\displaystyle {\phi}_{2′}=\angle 1,057^\circ-\angle 2^\circ=\angle -0,943^\circ[/math];
- [math]\displaystyle \Delta \dot{U}_{1′′4′} = \frac{P_{1′′4′н}\cdot R_{1-4}+Q_{1′′4′н}\cdot X_{1-4}}{|\dot U_{1′′}|} = \frac{10,719\cdot 4,8+5,454\cdot 16,2}{111,912} = 1,249[/math] кВ;
- [math]\displaystyle \delta \dot{U}_{1′′4′} = \frac{P_{1′′4′н}\cdot X_{1-4}-Q_{1′′4′н}\cdot R_{1-4}}{|\dot U_{1′′}|} = \frac{10,719\cdot 16,2-5,454\cdot 4,8}{111,912} = 1,318[/math] кВ;
- [math]\displaystyle \dot U_{4′}=|\dot U_{1′′}|-\Delta U_{1′′4′}-j\delta U_{1′′4′}=111,912-1,249-j1,318=110,671\angle -0,682^\circ[/math] кВ;
- [math]\displaystyle {\phi}_{4′}=\angle -0,682^\circ-\angle 2^\circ=\angle -2,682^\circ[/math].
Расчет уравнительных перетоков мощности
Между узлами потечет уравнительный переток мощности, обусловленный различием напряжений узлов [math]U_{1′} \text{ и } U_{1′′}, U_{2′} \text{ и } U_{2′′}, U_{4′} \text{ и } U_{4′′}[/math].
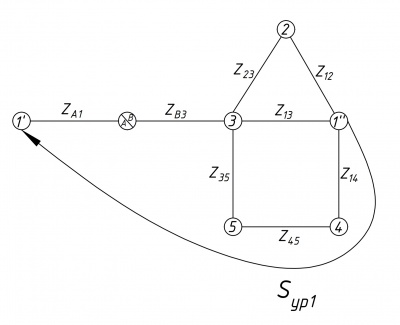
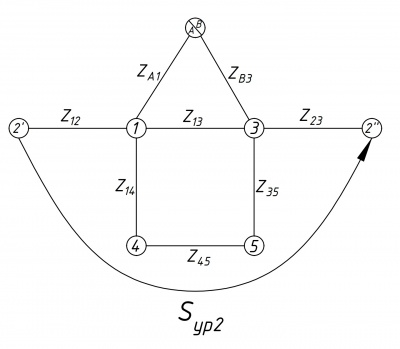
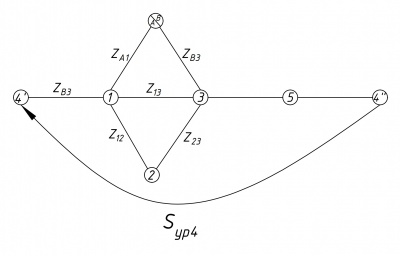
На рисунках 6, 7, 8 изображены эквивалентные схемы с уравнительными перетоками мощности.
Расчет эквивалентных сопротивлений:
- [math] \displaystyle\underline Z_{1′1′′}=\underline Z_{A-1}+\underline Z_{B-3}+\frac{\underline Z_{1-3}\cdot(\underline Z_{2-3}+\underline Z_{1-2})\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})}{\underline Z_{1-3}\cdot(\underline Z_{2-3}+\underline Z_{1-2})+\underline Z_{1-3}\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})+(\underline Z_{2-3}+\underline Z_{1-2})\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})}[/math];
- [math] \displaystyle \underline Z_{2-3}+\underline Z_{1-2}=2,4+j8,1+2,4+j8,1=4,8+j16,2\text{ Ом }[/math];
- [math] \displaystyle\underline Z_{1′1′′}=4,8+j16,2+2,4+j8,1+\frac{(3,6+j12,15)\cdot(4,8+j16,2)\cdot(9,6+j32,4)}{(3,6+j12,15)\cdot(4,8+j16,2)+(3,6+j12,15)\cdot(9,6+j32,4)+(4,8+j16,2)\cdot(9,6+j32,4)}+2,4+j8,1[/math];
- [math] \displaystyle\underline Z_{1′1′′}=8,894+j30,018\text{ Ом }[/math];
- [math] \displaystyle\underline Z_{2′2′′}=\underline Z_{1-2}+\frac{\underline Z_{1-3}\cdot(\underline Z_{A-1}+\underline Z_{B-3})\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})}{\underline Z_{1-3}\cdot(\underline Z_{A-1}+\underline Z_{B-3})+\underline Z_{1-3}\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})+(\underline Z_{A-1}+\underline Z_{B-3})\cdot(\underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5})}+\underline Z_{2-3}[/math];
- [math] \displaystyle \underline Z_{A-1}+\underline Z_{B-3}=4,8+j16,2+2,4+j8,1=7,2+j24,3\text{ Ом }[/math];
- [math] \displaystyle \underline Z_{1-4}+\underline Z_{4-5}+\underline Z_{3-5}=4,8+j16,2+1,2+j4,05+3,6+j12,15=9,6+j32,4\text{ Ом }[/math];
- [math] \displaystyle\underline Z_{2′2′′}=2,4+j8,1+\frac{(3,6+j12,15)\cdot(7,2+j24,3)\cdot(9,6+j32,4)}{(3,6+j12,15)\cdot(7,2+j24,3)+(3,6+j12,15)\cdot(9,6+j32,4)+(7,2+j24,3)\cdot(9,6+j32,4)}+2,4+j8,1[/math]
- [math] \displaystyle\underline Z_{2′2′′}=6,72+j22,68\text{ Ом }[/math]
- [math] \displaystyle\underline Z_{4′4′′}=\underline Z_{1-4}+\frac{\underline Z_{1-3}\cdot(\underline Z_{2-3}+\underline Z_{1-2})\cdot(\underline Z_{A-1}+\underline Z_{B-3})}{\underline Z_{1-3}\cdot(\underline Z_{2-3}+\underline Z_{1-2})+\underline Z_{1-3}\cdot(\underline Z_{A-1}+\underline Z_{B-3})+(\underline Z_{2-3}+\underline Z_{1-2})\cdot(\underline Z_{A-1}+\underline Z_{B-3})}+\underline Z_{3-5}+\underline Z_{4-5}[/math];
- [math] \displaystyle \underline Z_{A-1}+\underline Z_{B-3}=4,8+j16,2+2,4+j8,1=7,2+j24,3\text{ Ом }[/math];
- [math] \displaystyle\underline Z_{4′4′′}=4,8+j16,2+\frac{(3,6+j12,15)\cdot(4,8+j16,2)\cdot(7,2+j24,3)}{(3,6+j12,15)\cdot(4,8+j16,2)+(3,6+j12,15)\cdot(7,2+j24,3)+(4,8+j16,2)\cdot(7,2+j24,3)}+3,6+j12,15+1,2+j4,05[/math];
- [math] \displaystyle\underline Z_{4′4′′}=11,2+j37,8\text{ Ом }[/math].
Расчет уравнительных перетоков мощности:
- [math]\displaystyle \dot S_{ур1}= \frac{\dot U_{1′} + \dot U_{1′′}}{2}\cdot \frac{\hat U_{1′′}-\hat U_{1′}}{\hat Z_{1′1′′}}=\frac{111,544\angle -1,5^\circ+111,912 \angle -1,673^\circ}{2}\cdot \frac{111,912 \angle -1,673^\circ-111,544\angle -1,5^\circ}{8,894+j30,018}=12,56-j2,349\text{ МВА }[/math];
- [math]\displaystyle \dot S_{ур2}= \frac{\dot U_{2′} + \dot U_{2′′}}{2}\cdot \frac{\hat U_{2′}-\hat U_{2′′}}{\hat Z_{2′2′′}}=\frac{113,732\angle -0,943^\circ+113,528 \angle -0,563^\circ}{2}\cdot \frac{113,732\angle -0,943^\circ-113,528 \angle -0,563^\circ}{6,72+j22,68}=-3,198+j1,973\text{ МВА }[/math];
- [math]\displaystyle \dot S_{ур4}= \frac{\dot U_{4′} + \dot U_{4′′}}{2}\cdot \frac{\hat U_{4′}-\hat U_{4′′}}{\hat Z_{4′4′′}}=\frac{110,671\angle -2,682^\circ+110,487 \angle -2,316^\circ}{2}\cdot \frac{110,671\angle -2,682^\circ-110,487 \angle -2,316^\circ}{11,2+j37,8}=-1,752+j1,058\text{ МВА }[/math].
Данные для второй итерации
Потоки мощностей:
- [math]\displaystyle \dot S_{1′}=\dot S_{A1}-\dot S_{ур1}=25,45+j16,633-(12,56-j2,349)=12,89+j18,982 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{1′′}=\dot S_{S1′′}+\dot S_{ур1}=14,55+j3,367+12,56-j2,349=27,11+j1,018 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{2′}=\dot S_{12}+\dot S_{ур2}=33,665+j15,453+(-3,198+j1,973)=30,467+j17,426 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{2′′}=\dot S_{23}-\dot S_{ур2}=46,335+j24,547-(-3,198+j1,973)=12,89+j18,982 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{4′}=\dot S_{14}+\dot S_{ур4}=10,668+j6,024+(-1,752+j1,058)=8,916+j7,081 \text{ МВА }[/math];
- [math]\displaystyle \dot S_{4′′}=\dot S_{45}-\dot S_{ур4}=19,332+j8,976-(-1,752+j1,058)=21,084+j7,919 \text{ МВА }[/math].
Напряжения:
- [math]\displaystyle \dot{U}_{1}=111,714 \angle -1,586^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{2}=113,629 \angle -0,753^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{3}=110,801 \angle -1,934^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{4}=110,578 \angle -2,499^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{5}=111,02 \angle -1,995^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{1′}=111,544 \angle -1,5^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{1′′}=111,912 \angle -1,673^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{2′}=113,732 \angle -0,943^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{2′′}=113,528 \angle -0,563^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{4′}=110,671 \angle -2,682^\circ [/math] кВ;
- [math]\displaystyle \dot{U}_{4′′}=110,487 \angle -2,316^\circ [/math] кВ.
Потери в шунтах:
- [math]\displaystyle \dot{ΔS_{ш1′}} = \dot {|U_{1′}|}^{2}\cdot \frac {\hat Y_{A-1}}{2}={111,544}^{2}\cdot \frac {-j112,4}{2}\cdot 10^{-6}=-j0,699 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш1′′}} = \dot {|U_{1′′}|}^{2}\cdot\left( \frac {\hat Y_{1-2}}{2}+\frac {\hat Y_{1-3}}{2}+\frac {\hat Y_{1-4}}{2}\right)={111,912}^{2}\cdot \left( \frac {-j56,2}{2}+\frac {-j84,3}{2}+\frac {-j112,4}{2}\right)\cdot 10^{-6} = -j1,584 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш2′}} = \dot {|U_{2′}|}^{2}\cdot \frac {\hat Y_{1-2}}{2}={113,732}^{2}\cdot \frac {-j56,2}{2}\cdot 10^{-6}=-j0,363 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш2′′}} = \dot {|U_{2′′}|}^{2}\cdot \frac {\hat Y_{2-3}}{2}={113,528}^{2}\cdot \frac {-j56,2}{2}\cdot 10^{-6}=-j0,362 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш3}} = \dot {|U_{3}|}^{2}\cdot\left( \frac {\hat Y_{1-3}}{2}+\frac {\hat Y_{B-3}}{2}+\frac {\hat Y_{3-5}}{2}\frac {\hat Y_{2-3}}{2}\right)={110,801}^{2}\cdot \left( \frac {-j84,3}{2}+\frac {-j56,2}{2}+\frac {-j84,3}{2}+\frac {-j56,2}{2}\right)\cdot 10^{-6}=-j1,725 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш4′}} = \dot {|U_{4′}|}^{2}\cdot \frac {\hat Y_{1-4}}{2}={110,671}^{2}\cdot \frac {-j112,4}{2}\cdot 10^{-6}=-j0,688 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш4′′}} = \dot {|U_{4′′}|}^{2}\cdot \frac {\hat Y_{4-5}}{2}={110,487}^{2}\cdot \frac {-j28,1}{2}\cdot 10^{-6}=-j0,172 \text{ МВА } [/math];
- [math]\displaystyle \dot{ΔS_{ш5}} = \dot {|U_{5}|}^{2}\cdot\left( \frac {\hat Y_{4-5}}{2}+\frac {\hat Y_{3-5}}{2}\right)={111,02}^{2}\cdot \left( \frac {-j28,1}{2}+\frac {-j84,3}{2}\right)\cdot 10^{-6}=-j0,693 \text{ МВА } [/math].