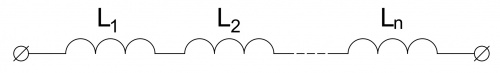Преобразование сложнозамкнутых электрических схем — различия между версиями
Agro (обсуждение | вклад) (→Разнос нагрузок на магистральном участке сети) |
Agro (обсуждение | вклад) (→Разнос нагрузок на магистральном участке сети) |
||
| Строка 106: | Строка 106: | ||
Составим 1 закон Кирхгофа для 1 и 2 узлов, | Составим 1 закон Кирхгофа для 1 и 2 узлов, | ||
| − | : <math>\displaystyle I_{2′} = -I_{1}-I_{n} \text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′} = -\dot I_{1}-\dot I_{n} \text{ ; }</math> |
| − | : <math>\displaystyle I_{2′′} = I_{2}-I_{2′}\text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′′} = \dot I_{2}-\dot I_{2′}\text{ ; }</math> |
Падение напряжения на участке сети 1 - 3, | Падение напряжения на участке сети 1 - 3, | ||
| − | : <math>\displaystyle U_{13} = I_{2′} \cdot Z_{12} - I_{2′′} \cdot Z_{23} \text{ . }</math> | + | : <math>\displaystyle \dot U_{13} = \dot I_{2′} \cdot \underline Z_{12} - \dot I_{2′′} \cdot \underline Z_{23} \text{ . }</math> |
Эквивалентный участок сети: | Эквивалентный участок сети: | ||
Составим 1 закон Кирхгофа для 1 узла, | Составим 1 закон Кирхгофа для 1 узла, | ||
| − | : <math>\displaystyle I_{13} = -I_{1}-I_{2′}-I_{n} \text{ ; }</math> | + | : <math>\displaystyle \dot I_{13} = -\dot I_{1}-\dot I_{2′}-\dot I_{n} \text{ ; }</math> |
Падение напряжения на участке сети 1 - 3: | Падение напряжения на участке сети 1 - 3: | ||
| − | : <math>\displaystyle U_{13} = I_{13} \cdot (Z_{12} + Z_{23}) \text{ . }</math> | + | : <math>\displaystyle \dot U_{13} = \dot I_{13} \cdot (\underline Z_{12} + \underline Z_{23}) \text{ . }</math> |
Приравняем падение напряжения на обоих участках сети, | Приравняем падение напряжения на обоих участках сети, | ||
| − | : <math>\displaystyle I_{2′} \cdot Z_{12} - (I_{2}-I_{2′}) \cdot Z_{23} = I_{13} \cdot (Z_{12} + Z_{23}) \text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′} \cdot \underline Z_{12} - (\dot I_{2}-\dot I_{2′}) \cdot \underline Z_{23} = \dot I_{13} \cdot (\underline Z_{12} + \underline Z_{23}) \text{ ; }</math> |
Подставим в последнее выражение найденные ранее соотношения, | Подставим в последнее выражение найденные ранее соотношения, | ||
| − | : <math>\displaystyle(-I_{1}-I_{n}) \cdot Z_{12} - (I_{2}-I_{2′}) \cdot Z_{23} = (-I_{1}-I_{2′}-I_{n}) \cdot (Z_{12} + Z_{23}) \text{ ; }</math> | + | : <math>\displaystyle(-\dot I_{1}-\dot I_{n}) \cdot \underline Z_{12} - (\dot I_{2}-\dot I_{2′}) \cdot \underline Z_{23} = (-\dot I_{1}-\dot I_{2′}-\dot I_{n}) \cdot (\underline Z_{12} + \underline Z_{23}) \text{ ; }</math> |
Раскроем скобки и преобразуем выражение, | Раскроем скобки и преобразуем выражение, | ||
| − | : <math>\displaystyle -I_{1} \cdot Z_{12} -I_{n} \cdot Z_{12} - I_{2} \cdot Z_{23} + I_{2′} \cdot Z_{23} = -I_{1} \cdot Z_{12}-I_{1} \cdot Z_{23} - I_{2′} \cdot Z_{12} - I_{2′} \cdot Z_{23} - I_{n} \cdot Z_{12} - I_{n} \cdot Z_{23} \text{ ; }</math> | + | : <math>\displaystyle -\dot I_{1} \cdot \underline Z_{12} -\dot I_{n} \cdot \underline Z_{12} - \dot I_{2} \cdot \underline Z_{23} + \dot I_{2′} \cdot \underline Z_{23} = -\dot I_{1} \cdot \underline Z_{12}-\dot I_{1} \cdot \underline Z_{23} - \dot I_{2′} \cdot \underline Z_{12} - \dot I_{2′} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{12} - \dot I_{n} \cdot \underline Z_{23} \text{ ; }</math> |
| − | : <math>\displaystyle - I_{2} \cdot Z_{23} + I_{2′} \cdot Z_{23} = -I_{1} \cdot Z_{23} - I_{2′} \cdot Z_{12} - I_{2′} \cdot Z_{23} - I_{n} \cdot Z_{23} \text{ ; }</math> | + | : <math>\displaystyle - \dot I_{2} \cdot \underline Z_{23} + \dot I_{2′} \cdot \underline Z_{23} = -\dot I_{1} \cdot \underline Z_{23} - \dot I_{2′} \cdot \underline Z_{12} - \dot I_{2′} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{23} \text{ ; }</math> |
| − | : <math>\displaystyle I_{2′} \cdot (Z_{12} + Z_{23}) = I_{2} \cdot Z_{23} - I_{2′} \cdot Z_{23} - I_{1} \cdot Z_{23} - I_{n} \cdot Z_{23}\text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′} \cdot (\underline Z_{12} + \underline Z_{23}) = \dot I_{2} \cdot \underline Z_{23} - \dot I_{2′} \cdot \underline Z_{23} - \dot I_{1} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{23}\text{ ; }</math> |
| − | + | Так как. : <math>\displaystyle \dot I_{2′} = -\dot I_{1}-\dot I_{n}</math>, то | |
| − | : <math>\displaystyle I_{2′} \cdot (Z_{12} + Z_{23}) = I_{2} \cdot Z_{23} + I_{1} \cdot Z_{23} + I_{n} \cdot Z_{23} - I_{1} \cdot Z_{23} - I_{n} \cdot Z_{23}\text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′} \cdot (\underline Z_{12} + \underline Z_{23}) = \dot I_{2} \cdot \underline Z_{23} + \dot I_{1} \cdot \underline Z_{23} + \dot I_{n} \cdot \underline Z_{23} - \dot I_{1} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{23}\text{ ; }</math> |
| − | : <math>\displaystyle I_{2′} \cdot (Z_{12} + Z_{23}) = I_{2} \cdot Z_{23} \text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′} \cdot (\underline Z_{12} + \underline Z_{23}) = \dot I_{2} \cdot \underline Z_{23} \text{ ; }</math> |
| − | : <math>\displaystyle I_{2′} = \frac{I_{2} \cdot Z_{23}}{Z_{12}+Z_{23}} \text{ ; }</math> | + | : <math>\displaystyle \dot I_{2′} = \frac{\dot I_{2} \cdot \underline Z_{23}}{\underline Z_{12}+\underline Z_{23}} \text{ ; }</math> |
| − | + | Так как : <math>\displaystyle \dot I_{2′} = \dot I_{2}-\dot I_{2′′}</math>, то | |
| − | : <math>\displaystyle I_{2} \cdot Z_{12} + I_{2} \cdot Z_{23} - I_{2′′} \cdot Z_{12} - I_{2′′} \cdot Z_{23} = I_{2} \cdot Z_{23} \text{ ; }</math> | + | : <math>\displaystyle \dot I_{2} \cdot \underline Z_{12} + \dot I_{2} \cdot \underline Z_{23} - \dot I_{2′′} \cdot \underline Z_{12} - \dot I_{2′′} \cdot \underline Z_{23} = \dot I_{2} \cdot \underline Z_{23} \text{ ; }</math> |
| − | : <math>\displaystyle I_{2} \cdot Z_{12} = I_{2′′} \cdot (Z_{12} + Z_{23}) \text{ ; }</math> | + | : <math>\displaystyle \dot I_{2} \cdot \underline Z_{12} = \dot I_{2′′} \cdot (\underline Z_{12} + \underline Z_{23}) \text{ ; }</math> |
| − | : <math>\displaystyle I_{2′′} = \frac{I_{2} \cdot Z_{12}}{Z_{12}+Z_{23}} \text{ . }</math> | + | : <math>\displaystyle \dot I_{2′′} = \frac{\dot I_{2} \cdot \underline Z_{12}}{\underline Z_{12}+\underline Z_{23}} \text{ . }</math> |
Применим сопряжение с обеих сторон для каждой формулы и домножим на U, | Применим сопряжение с обеих сторон для каждой формулы и домножим на U, | ||
| − | : <math>\displaystyle \overset{*}{I_{2′}} \cdot U_{1} = \frac{\overset{*}{I_{2}} \cdot U_{1} \cdot \hat Z_{23}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } \overset{*}{I_{2′′}} \cdot U_{3} = \frac{\overset{*}{I_{2}} \cdot U_{3} \cdot \hat Z_{12}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } </math> | + | : <math>\displaystyle \overset{*}{\dot I_{2′}} \cdot \dot U_{1} = \frac{\overset{*}{\dot I_{2}} \cdot \dot U_{1} \cdot \hat Z_{23}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } \overset{*}{\dot I_{2′′}} \cdot \dot U_{3} = \frac{\overset{*}{\dot I_{2}} \cdot \dot U_{3} \cdot \hat Z_{12}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } </math> |
| − | + | Так как : <math>\displaystyle S = \overset{*}{I} \cdot U</math>, то финальные формулы имеют вид: | |
| − | : <math>\displaystyle {S_{2′}} = \frac{{S_{2}}\cdot \hat Z_{23}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } {S_{2′′}} = \frac{{S_{2}}\cdot \hat Z_{12}}{\hat Z_{12} + \hat Z_{23}} \text{ | + | : <math>\displaystyle {\dot S_{2′}} = \frac{{\dot S_{2}}\cdot \hat Z_{23}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } {\dot S_{2′′}} = \frac{{\dot S_{2}}\cdot \hat Z_{12}}{\hat Z_{12} + \hat Z_{23}} \text{ . } </math> |
== Разнос нагрузки из центра звезды == | == Разнос нагрузки из центра звезды == | ||
Версия 21:24, 1 апреля 2020
В статье приводится описание методов эквивалентирования сложнозамкнутых электрических сетей, при расчёте параметров установившегося режима электрической сети.
Содержание
Общие положения
Для расчётов параметров установившихся режимов сложнозамкнутых электрических сетей может быть использован метод преобразования сети. Суть этого метода сводится к приведению сети к более простому виду. Упрощенная сеть рассчитывается с использованием известных методов расчёта разомкнутых сетей и сетей с двухсторонним питанием и затем производится обратное преобразование сети к исходному виду. При использовании метода преобразования применяются приемы разноса нагрузок по концам участка сети и из центра звезды, объединения концевых источников питания и нагрузок, преобразования пассивных частей схем электрической сети. Метод преобразования должен применяться с соблюдением условия неизменности параметров установившегося режима сети, внешней по отношению к преобразуемой ее части.
Преобразование пассивных элементов схемы
Последовательное сложение элементов
При последовательном соединении:
- [math]\displaystyle I={I}_{1}={I}_{2}={I}_{n}[/math]
- [math]\displaystyle U={U}_{1}+{U}_{2}+...+{U}_{n}[/math]
- Последовательное сложение резисторов
- [math]\displaystyle {R}_{экв}={R}_{1}+{R}_{2}+...+{R}_{n}[/math]
- Последовательное сложение катушек индуктивности
- [math]\displaystyle {L}_{экв}={L}_{1}+{L}_{2}+...+{L}_{n} =\gt {j} \cdot {X}_{{L}_{экв}}={j} \cdot {X}_{{L}_{1}}+{j} \cdot {X}_{{L}_{2}}+...+{j} \cdot {X}_{{L}_{n}}[/math]
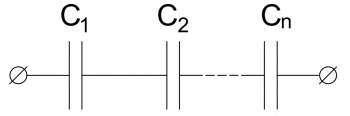
- Последовательное сложение конденсаторов
- [math]\displaystyle \frac{1}{{C}_{экв}}=\frac{1}{{C}_{1}}+\frac{1}{{C}_{2}}+...+\frac{1}{{C}_{n}} =\gt {j} \cdot {X}_{{C}_{экв}}={j} \cdot {X}_{{C}_{1}}+{j} \cdot {X}_{{C}_{2}}+...+{j} \cdot {X}_{{C}_{n}}[/math]
Параллельное сложение элементов
При параллельном соединении:
- [math]\displaystyle U={U}_{1}={U}_{2}={U}_{n}[/math]
- [math]\displaystyle I={I}_{1}+{I}_{2}+...+{I}_{n}[/math]
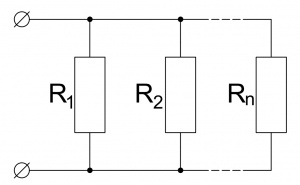
- Параллельное сложение резисторов
- [math]\displaystyle \frac{1}{{R}_{экв}}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+...+\frac{1}{{R}_{n}}[/math]
или
- [math]\displaystyle {g}_{экв}={g}_{1}+{g}_{2}+...+{g}_{n}[/math]
где [math]\displaystyle g = \frac{1}{R}[/math] — проводимость.
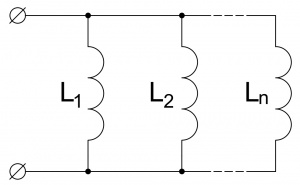
- Параллельное сложение катушек индуктивности
- [math]\displaystyle \frac{1}{{L}_{экв}}=\frac{1}{{L}_{1}}+\frac{1}{{L}_{2}}+...+\frac{1}{{L}_{n}} =\gt \frac{1}{{j} \cdot {X}_{{L}_{экв}}}=\frac{1}{{j} \cdot {X}_{{L}_{1}}}+\frac{1}{{j} \cdot {X}_{{L}_{2}}}+...+\frac{1}{{j} \cdot {L}_{{L}_{n}}} [/math]
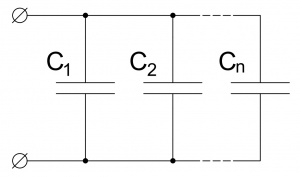
- Параллельное сложение конденсаторов
- [math]\displaystyle {C}_{экв}={C}_{1}+{C}_{2}+...+{C}_{n} =\gt \frac{1}{{j} \cdot {X}_{{C}_{экв}}}=\frac{1}{{j} \cdot {X}_{{C}_{1}}}+\frac{1}{{j} \cdot {X}_{{C}_{2}}}+...+\frac{1}{{j} \cdot {X}_{{C}_{n}}}[/math]
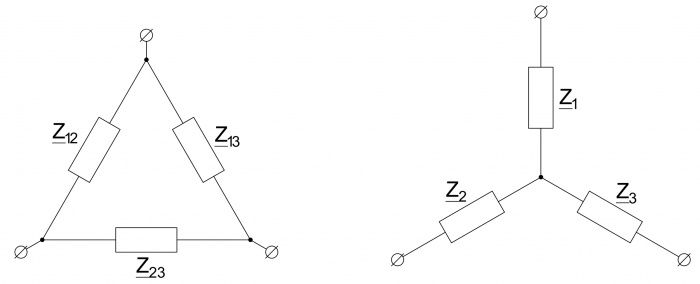
Преобразование треугольник-звезда
Преобразование треугольник-звезда — способ преобразования участка линейной электрической цепи в виде треугольника к эквивалентному участку цепи в виде звезды. Возможность данного преобразования обусловлена тем, что в обоих случаях потенциалы между одноименными точками, а также токи подтекающие к ним не изменятся.
- [math]\displaystyle \underline{Z}_{1}=\frac{\underline{Z}_{12} \cdot \underline{Z}_{13}}{\underline{Z}_{12}+\underline{Z}_{23}+\underline{Z}_{13}}[/math]
- [math]\displaystyle \underline{Z}_{2}=\frac{\underline{Z}_{12} \cdot \underline{Z}_{23}}{\underline{Z}_{12}+\underline{Z}_{23}+\underline{Z}_{13}}[/math]
- [math]\displaystyle \underline{Z}_{3}=\frac{\underline{Z}_{23} \cdot \underline{Z}_{13}}{\underline{Z}_{12}+\underline{Z}_{23}+\underline{Z}_{13}}[/math]
- Преобразование звезда-треугольник
- [math]\displaystyle \underline{Z}_{12}=\underline{Z}_{1}+\underline{Z}_{2}+\frac{\underline{Z}_{1} \cdot \underline{Z}_{2}}{\underline{Z}_{3}}[/math]
- [math]\displaystyle \underline{Z}_{13}=\underline{Z}_{1}+\underline{Z}_{3}+\frac{\underline{Z}_{1} \cdot \underline{Z}_{3}}{\underline{Z}_{2}}[/math]
- [math]\displaystyle \underline{Z}_{23}=\underline{Z}_{2}+\underline{Z}_{3}+\frac{\underline{Z}_{2} \cdot \underline{Z}_{3}}{\underline{Z}_{1}}[/math]
Исключение нагрузочных и генераторных узлов
Разнос нагрузок из любого узла сети должен выполняться так, чтобы преобразование электрической сети было эквивалентным. Эквивалентность преобразования соблюдается, если в результате не изменяются параметры режима в той части схемы, которая не подвергалась преобразованию.
Разнос нагрузок на магистральном участке сети
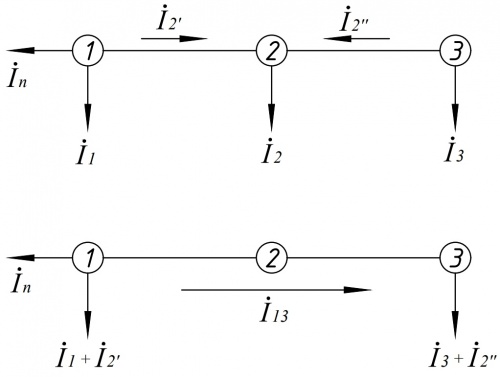
Пусть дан участок сети 1-2-3, представленный на Рисунке 1.
В узлах даны токи инъекции. Выполним разнос нагрузки узла 2 между узлами 1 и 3.
Исходный участок сети:
Составим 1 закон Кирхгофа для 1 и 2 узлов,
- [math]\displaystyle \dot I_{2′} = -\dot I_{1}-\dot I_{n} \text{ ; }[/math]
- [math]\displaystyle \dot I_{2′′} = \dot I_{2}-\dot I_{2′}\text{ ; }[/math]
Падение напряжения на участке сети 1 - 3,
- [math]\displaystyle \dot U_{13} = \dot I_{2′} \cdot \underline Z_{12} - \dot I_{2′′} \cdot \underline Z_{23} \text{ . }[/math]
Эквивалентный участок сети:
Составим 1 закон Кирхгофа для 1 узла,
- [math]\displaystyle \dot I_{13} = -\dot I_{1}-\dot I_{2′}-\dot I_{n} \text{ ; }[/math]
Падение напряжения на участке сети 1 - 3:
- [math]\displaystyle \dot U_{13} = \dot I_{13} \cdot (\underline Z_{12} + \underline Z_{23}) \text{ . }[/math]
Приравняем падение напряжения на обоих участках сети,
- [math]\displaystyle \dot I_{2′} \cdot \underline Z_{12} - (\dot I_{2}-\dot I_{2′}) \cdot \underline Z_{23} = \dot I_{13} \cdot (\underline Z_{12} + \underline Z_{23}) \text{ ; }[/math]
Подставим в последнее выражение найденные ранее соотношения,
- [math]\displaystyle(-\dot I_{1}-\dot I_{n}) \cdot \underline Z_{12} - (\dot I_{2}-\dot I_{2′}) \cdot \underline Z_{23} = (-\dot I_{1}-\dot I_{2′}-\dot I_{n}) \cdot (\underline Z_{12} + \underline Z_{23}) \text{ ; }[/math]
Раскроем скобки и преобразуем выражение,
- [math]\displaystyle -\dot I_{1} \cdot \underline Z_{12} -\dot I_{n} \cdot \underline Z_{12} - \dot I_{2} \cdot \underline Z_{23} + \dot I_{2′} \cdot \underline Z_{23} = -\dot I_{1} \cdot \underline Z_{12}-\dot I_{1} \cdot \underline Z_{23} - \dot I_{2′} \cdot \underline Z_{12} - \dot I_{2′} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{12} - \dot I_{n} \cdot \underline Z_{23} \text{ ; }[/math]
- [math]\displaystyle - \dot I_{2} \cdot \underline Z_{23} + \dot I_{2′} \cdot \underline Z_{23} = -\dot I_{1} \cdot \underline Z_{23} - \dot I_{2′} \cdot \underline Z_{12} - \dot I_{2′} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{23} \text{ ; }[/math]
- [math]\displaystyle \dot I_{2′} \cdot (\underline Z_{12} + \underline Z_{23}) = \dot I_{2} \cdot \underline Z_{23} - \dot I_{2′} \cdot \underline Z_{23} - \dot I_{1} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{23}\text{ ; }[/math]
Так как. : [math]\displaystyle \dot I_{2′} = -\dot I_{1}-\dot I_{n}[/math], то
- [math]\displaystyle \dot I_{2′} \cdot (\underline Z_{12} + \underline Z_{23}) = \dot I_{2} \cdot \underline Z_{23} + \dot I_{1} \cdot \underline Z_{23} + \dot I_{n} \cdot \underline Z_{23} - \dot I_{1} \cdot \underline Z_{23} - \dot I_{n} \cdot \underline Z_{23}\text{ ; }[/math]
- [math]\displaystyle \dot I_{2′} \cdot (\underline Z_{12} + \underline Z_{23}) = \dot I_{2} \cdot \underline Z_{23} \text{ ; }[/math]
- [math]\displaystyle \dot I_{2′} = \frac{\dot I_{2} \cdot \underline Z_{23}}{\underline Z_{12}+\underline Z_{23}} \text{ ; }[/math]
Так как : [math]\displaystyle \dot I_{2′} = \dot I_{2}-\dot I_{2′′}[/math], то
- [math]\displaystyle \dot I_{2} \cdot \underline Z_{12} + \dot I_{2} \cdot \underline Z_{23} - \dot I_{2′′} \cdot \underline Z_{12} - \dot I_{2′′} \cdot \underline Z_{23} = \dot I_{2} \cdot \underline Z_{23} \text{ ; }[/math]
- [math]\displaystyle \dot I_{2} \cdot \underline Z_{12} = \dot I_{2′′} \cdot (\underline Z_{12} + \underline Z_{23}) \text{ ; }[/math]
- [math]\displaystyle \dot I_{2′′} = \frac{\dot I_{2} \cdot \underline Z_{12}}{\underline Z_{12}+\underline Z_{23}} \text{ . }[/math]
Применим сопряжение с обеих сторон для каждой формулы и домножим на U,
- [math]\displaystyle \overset{*}{\dot I_{2′}} \cdot \dot U_{1} = \frac{\overset{*}{\dot I_{2}} \cdot \dot U_{1} \cdot \hat Z_{23}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } \overset{*}{\dot I_{2′′}} \cdot \dot U_{3} = \frac{\overset{*}{\dot I_{2}} \cdot \dot U_{3} \cdot \hat Z_{12}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } [/math]
Так как : [math]\displaystyle S = \overset{*}{I} \cdot U[/math], то финальные формулы имеют вид:
- [math]\displaystyle {\dot S_{2′}} = \frac{{\dot S_{2}}\cdot \hat Z_{23}}{\hat Z_{12} + \hat Z_{23}} \text{ ; } {\dot S_{2′′}} = \frac{{\dot S_{2}}\cdot \hat Z_{12}}{\hat Z_{12} + \hat Z_{23}} \text{ . } [/math]
Разнос нагрузки из центра звезды
Объединение источников питания
Примечания
1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник для Вузов. — 8. — М.: Высшая школа, 1984. — 559 с.