Моделирование дуговых поперечных несимметричных режимов в RastrWin — различия между версиями
Windsl (обсуждение | вклад) м (→Модели) |
(→Общая часть) |
||
| (не показаны 104 промежуточные версии 3 участников) | |||
| Строка 4: | Строка 4: | ||
Такие модели необходимы для расчётов дуговых [[короткое замыкание|коротких замыканий]]. | Такие модели необходимы для расчётов дуговых [[короткое замыкание|коротких замыканий]]. | ||
| − | = | + | = Оценка сопротивления дуги = |
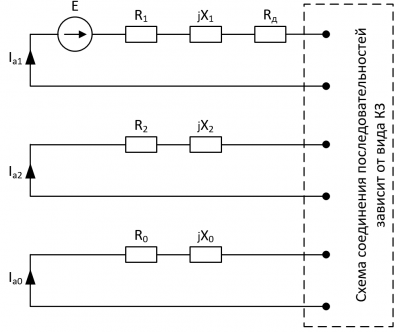
| + | [[Файл:Комплексная схема симметричных составляющих для всех видов КЗ.png|thumb|400px|Рисунок 1. Комплексная схема симметричных составляющих для всех видов КЗ.]] | ||
| + | По расчётным данным металлического короткого замыкания можно оценить сопротивление дуги с учётом того, что: | ||
| + | * Есть только периодическая составляющая тока короткого замыкания. | ||
| + | * Сопротивление дуги с течением времени постоянно. | ||
| + | * ЭДС совпадает по направлению с осью действительных чисел. | ||
| − | + | Для каждого вида короткого замыкания можно вывести уравнение для оценки сопротивления дуги. | |
| − | + | Пусть дуга это три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный <math>I_a</math> по модулю. | |
| − | + | Неизвестные: <math>R_a, I_a</math> | |
| − | + | Обозначения: | |
| + | $$ | ||
| + | \dot{I}_a = I_a \cdot \left(\cos(\varphi) + j \cdot \sin(\varphi) \right), | ||
| + | $$ | ||
| − | = | + | $$ |
| + | \dot{E} = E, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \dot{Z}_0 = R_0 + j \cdot X_0, | ||
| + | $$ | ||
| + | $$ | ||
| + | \dot{Z}_1 = R_1 + j \cdot X_1, | ||
| + | $$ | ||
| − | = | + | $$ |
| + | \dot{Z}_2 = R_2 + j \cdot X_2. | ||
| + | $$ | ||
| − | + | =Короткие замыкания на землю= | |
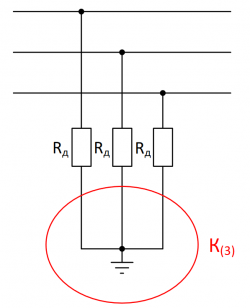
| − | + | ==Трехфазное КЗ== | |
| + | [[Файл:Трехфазное КЗ через сопротивление дуги.png|thumb|250px|Рисунок 2. Моделирование поперечной несимметрии при К(3).]] | ||
| + | |||
| + | Система для решения: | ||
| + | $$ | ||
| + | \left\{ | ||
| + | \begin{array}{@{}l@{}} | ||
| + | \dot{E} = \dot{I}_a \cdot (R_a + \dot{Z}_1), \\ | ||
| + | R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * Подставим <math>R_a</math> из второго уравнения в первое и выполним замену: | ||
| + | $$ | ||
| + | K = U \cdot L | ||
| + | $$ | ||
| + | $$ | ||
| + | B = 1 | ||
| + | $$ | ||
| + | $$ | ||
| + | R^\prime = R_1 | ||
| + | $$ | ||
| + | $$ | ||
| + | X^\prime = X_1 | ||
| + | $$ | ||
| + | |||
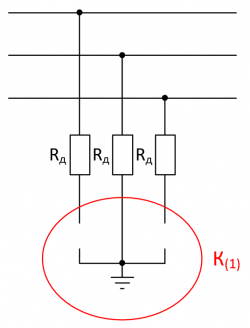
| + | ==Однофазное КЗ== | ||
| + | [[Файл:Однофазное КЗ на землю через сопротивление дуги.png|thumb|250px|Рисунок 3. Моделирование поперечной несимметрии при К(1).]] | ||
| + | |||
| + | Система для решения: | ||
| + | $$ | ||
| + | \left\{ | ||
| + | \begin{array}{@{}l@{}} | ||
| + | \dot{E} = \frac{1}{3} \cdot \dot{I}_a \cdot (R_a + \dot{Z}_0 + \dot{Z}_1 + \dot{Z}_2), \\ | ||
| + | R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * Подставим <math>R_a</math> из второго уравнения в первое и выполним замену: | ||
| + | $$ | ||
| + | K = U \cdot L | ||
| + | $$ | ||
| + | $$ | ||
| + | B = \frac{1}{3} | ||
| + | $$ | ||
| + | $$ | ||
| + | R^\prime = R_0 + R_1 + R_2 | ||
| + | $$ | ||
| + | $$ | ||
| + | X^\prime = X_0 + X_1 + X_2 | ||
| + | $$ | ||
| + | |||
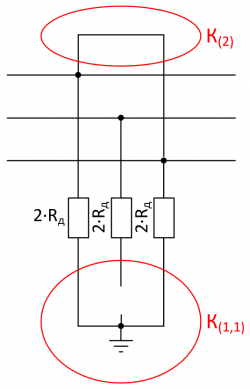
| + | ==Двухфазное КЗ на землю== | ||
| + | [[Файл:Двухфазное КЗ на землю через сопротивление дуги.png|thumb|250px|Рисунок 4. Моделирование поперечной несимметрии при К(1,1).]] | ||
| + | |||
| + | Система для решения: | ||
| + | $$ | ||
| + | \left\{ | ||
| + | \begin{array}{@{}l@{}} | ||
| + | \dot{E} = - \frac{1}{3} \cdot \dot{I}_a \cdot \left(2 \cdot R_a + \dot{Z}_0 + \dot{Z}_1 + \frac{\dot{Z}_0 \cdot \dot{Z}_1}{\dot{Z}_2}\right), \\ | ||
| + | 2 \cdot R_a = \frac{2 \cdot U \cdot L}{I_a} = \frac{K}{I_a} | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * Подставим <math>R_a</math> из второго уравнения в первое и выполним замену: | ||
| + | $$ | ||
| + | K = 2 \cdot U \cdot L | ||
| + | $$ | ||
| + | $$ | ||
| + | B = - \frac{1}{3} | ||
| + | $$ | ||
| + | $$ | ||
| + | R^\prime = R_0 + R_1 + \frac{R_0 R_1 R_2 - X_0 X_1 R_2 + R_0 X_1 X_2 + X_0 R_1 X_2}{R_2^{2} + X_2^{2}} | ||
| + | $$ | ||
| + | $$ | ||
| + | X^\prime = X_0 + X_1 + \frac{R_0 X_1 R_2 + X_0 R_1 R_2 - R_0 R_1 X_2 + X_0 X_1 X_2}{R_2^{2} + X_2^{2}} | ||
| + | $$ | ||
| + | |||
| + | ==Общая часть== | ||
| + | Общая система для решения: | ||
| + | $$ | ||
| + | \left\{ | ||
| + | \begin{array}{@{}l@{}} | ||
| + | \dot{E} = B \cdot \dot{I}_a \cdot (R_a + R^\prime + j \cdot X^\prime), \\ | ||
| + | R_a = \frac{K}{I_a} | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | Решение: | ||
| + | |||
| + | $$ | ||
| + | E = B \cdot I_a \cdot \left(\cos(\varphi) + j \cdot \sin(\varphi) \right) \cdot \left(\frac{K}{I_a} + R^\prime + j \cdot X^\prime \right) | ||
| + | $$ | ||
| + | |||
| + | * Внесём <math>I_a</math> в скобки и разделим обе части на <math>(\cos(\varphi) + j \cdot \sin(\varphi))</math>: | ||
| + | |||
| + | $$ | ||
| + | \frac{E}{\cos(\varphi) + j \cdot \sin(\varphi)} = B \cdot \left(K + I_a \cdot R^\prime + j \cdot I_a \cdot X^\prime \right) | ||
| + | $$ | ||
| + | |||
| + | * Преобразуем: | ||
| + | |||
| + | $$ | ||
| + | E \cdot (\cos(\varphi) - j \cdot \sin(\varphi)) = B \cdot \left(K + I_a \cdot R^\prime + j \cdot I_a \cdot X^\prime \right) | ||
| + | $$ | ||
| + | |||
| + | * Раскроем скобки, приравняем действительные и мнимые компоненты: | ||
| + | |||
| + | $$ | ||
| + | \left\{\begin{array}{@{}B@{}} | ||
| + | \cos(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) , \\ | ||
| + | -\sin(\varphi) \cdot E = B \cdot I_a \cdot X^\prime | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * Выразим <math>I_a</math> из второго уравнения: | ||
| + | $$ | ||
| + | I_a = -\sin(\varphi) \cdot \frac{E}{B \cdot X^\prime} | ||
| + | $$ | ||
| + | |||
| + | * Подставим <math>I_a</math> в первое уравнение: | ||
| + | |||
| + | $$ | ||
| + | \cos(\varphi) \cdot E = B \cdot K - B \cdot \sin(\varphi) \cdot \frac{E \cdot R^\prime}{B \cdot X^\prime} | ||
| + | $$ | ||
| + | |||
| + | * Домножим на <math>X^\prime</math>, приведем подобные: | ||
| + | |||
| + | $$ | ||
| + | \cos(\varphi) \cdot E \cdot X^\prime = B \cdot K \cdot X^\prime - \sin(\varphi) \cdot E \cdot R^\prime | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \cos(\varphi) \cdot E \cdot X^\prime + \sin(\varphi) \cdot E \cdot R^\prime = B \cdot K \cdot X^\prime | ||
| + | $$ | ||
| + | |||
| + | * Введем переменные: | ||
| + | |||
| + | $$ | ||
| + | A = \sqrt{(E \cdot X^\prime)^2 + (E \cdot R^\prime)^2} | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \alpha = atan2\left( (E \cdot R^\prime), (E \cdot X^\prime) \right) | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \cos(\alpha) = \frac{E \cdot X^\prime}{A} | ||
| + | $$ | ||
| + | $$ | ||
| + | \sin(\alpha) = \frac{E \cdot R^\prime}{A} | ||
| + | $$ | ||
| + | |||
| + | * Подставим переменные, разделив уравнение на <math>A</math>: | ||
| + | |||
| + | $$ | ||
| + | \cos(\varphi) \cdot \cos(\alpha) + \sin(\varphi) \cdot \sin(\alpha) = \frac{B \cdot K \cdot X^\prime}{A} | ||
| + | $$ | ||
| + | |||
| + | * Записанное слева — косинус разности: | ||
| + | $$ | ||
| + | \cos(\varphi - \alpha) = \frac{B \cdot K \cdot X^\prime}{A} | ||
| + | $$ | ||
| + | |||
| + | * Решим относительно <math>\varphi</math>: | ||
| + | |||
| + | $$ | ||
| + | \varphi = \alpha \pm acos \left( \frac{B \cdot K \cdot X^\prime}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} | ||
| + | $$ | ||
| + | |||
| + | * <math>I_a</math> находится из первого уравнения системы: | ||
| + | $$ | ||
| + | \left\{\begin{array}{@{}B@{}} | ||
| + | \cos(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) , \\ | ||
| + | -\sin(\varphi) \cdot E = B \cdot I_a \cdot X^\prime | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * И подставляется в выражение: | ||
| + | $$ | ||
| + | R_a = \frac{K}{I_a} | ||
| + | $$ | ||
| + | |||
| + | = Короткие замыкания без земли = | ||
| + | |||
| + | ==Двухфазное КЗ== | ||
| + | |||
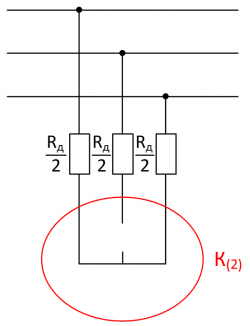
| + | [[Файл:Междуфазное КЗ через сопротивление дуги.png|thumb|250px|Рисунок 5. Моделирование поперечной несимметрии при К(2).]] | ||
| + | |||
| + | Система для решения: | ||
| + | |||
| + | $$ | ||
| + | \left\{ | ||
| + | \begin{array}{@{}l@{}} | ||
| + | \dot{E} = j\frac{1}{\sqrt{3}} \cdot \dot{I}_a \cdot (\frac{R_a}{2} + \dot{Z}_1 + \dot{Z}_2), \\ | ||
| + | \frac{R_a}{2} = \frac{U \cdot L}{2 \cdot I_a} = \frac{K}{I_a} | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * Подставим <math>R_a</math> из второго уравнения в первое и выполним замену: | ||
| + | $$ | ||
| + | K =\frac{U \cdot L}{2} | ||
| + | $$ | ||
| + | $$ | ||
| + | B =\frac{1}{\sqrt{3}} | ||
| + | $$ | ||
| + | $$ | ||
| + | R^\prime = R_1 + R_2 | ||
| + | $$ | ||
| + | $$ | ||
| + | X^\prime = X_1 + X_2 | ||
| + | $$ | ||
| + | |||
| + | Решение: | ||
| + | |||
| + | $$ | ||
| + | E = j\cdot B \cdot I_a \cdot \left(\cos(\varphi) + j \cdot \sin(\varphi) \right) \cdot \left(\frac{K}{I_a} + R^\prime + j \cdot X^\prime \right) | ||
| + | $$ | ||
| + | |||
| + | * Внесём <math>I_a</math> в скобки и разделим обе части на <math>(\cos(\varphi) + j \cdot \sin(\varphi))</math>: | ||
| + | |||
| + | $$ | ||
| + | \frac{E}{\cos(\varphi) + j \cdot \sin(\varphi)} = j \cdot B \cdot \left(K + I_a \cdot R^\prime + j \cdot I_a \cdot X^\prime \right) | ||
| + | $$ | ||
| + | |||
| + | * Преобразуем: | ||
| + | |||
| + | $$ | ||
| + | E \cdot (\cos(\varphi) - j \cdot \sin(\varphi)) = j \cdot B \cdot (K + I_a \cdot R^\prime) - B \cdot I_a \cdot X^\prime | ||
| + | $$ | ||
| + | |||
| + | * Раскроем скобки, приравняем действительные и мнимые компоненты: | ||
| + | |||
| + | $$ | ||
| + | \left\{\begin{array}{@{}l@{}} | ||
| + | \cos(\varphi) \cdot E = - B \cdot I_a \cdot X^\prime, \\ | ||
| + | -\sin(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * Выразим <math>I_a</math> из первого уравнения: | ||
| + | $$ | ||
| + | I_a = - \cos(\varphi) \cdot \frac{E}{B \cdot X^\prime} | ||
| + | $$ | ||
| + | |||
| + | * Подставим <math>I_a</math> во второе уравнение: | ||
| + | |||
| + | $$ | ||
| + | -\sin(\varphi) \cdot E = B \cdot K - B \cdot \cos(\varphi) \cdot \frac{E \cdot R^\prime}{B \cdot X^\prime} | ||
| + | $$ | ||
| + | |||
| + | * Домножим на <math>X^\prime</math>, приведем подобные: | ||
| + | |||
| + | $$ | ||
| + | -\sin(\varphi) \cdot E \cdot X^\prime = B \cdot K \cdot X^\prime - \cos(\varphi) \cdot E \cdot R^\prime | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \cos(\varphi) \cdot E \cdot R^\prime - \sin(\varphi) \cdot E \cdot X^\prime = B \cdot K \cdot X^\prime | ||
| + | $$ | ||
| + | |||
| + | * Введем переменные: | ||
| + | |||
| + | $$ | ||
| + | A = \sqrt{(E \cdot R^\prime)^2 + (E \cdot X^\prime)^2} | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \alpha = atan2\left( (E \cdot X^\prime), (E \cdot R^\prime) \right) | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \cos(\alpha) = \frac{E \cdot R^\prime}{A} | ||
| + | $$ | ||
| + | $$ | ||
| + | \sin(\alpha) = \frac{E \cdot X^\prime}{A} | ||
| + | $$ | ||
| + | |||
| + | * Подставим переменные, разделив уравнение на <math>A</math>: | ||
| + | |||
| + | $$ | ||
| + | \cos(\varphi) \cdot \cos(\alpha) - \sin(\varphi) \cdot \sin(\alpha) = \frac{B \cdot K \cdot X^\prime}{A} | ||
| + | $$ | ||
| + | |||
| + | * Записанное слева — косинус разности: | ||
| + | $$ | ||
| + | \cos(\varphi + \alpha) = \frac{B \cdot K \cdot X^\prime}{A} | ||
| + | $$ | ||
| + | |||
| + | * Решим относительно <math>\varphi</math>: | ||
| + | |||
| + | $$ | ||
| + | \varphi = - \alpha \pm acos \left( \frac{B \cdot K \cdot X^\prime}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} | ||
| + | $$ | ||
| + | |||
| + | * <math>I_a</math> находится из второго уравнения системы: | ||
| + | $$ | ||
| + | \left\{\begin{array}{@{}l@{}} | ||
| + | \cos(\varphi) \cdot E = - B \cdot I_a \cdot X^\prime, \\ | ||
| + | -\sin(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) | ||
| + | \end{array}\right. | ||
| + | $$ | ||
| + | |||
| + | * И подставляется в выражение: | ||
| + | $$ | ||
| + | R_a = \frac{K}{I_a} | ||
| + | $$ | ||
Текущая версия на 21:18, 7 апреля 2023
В статье описан подход к моделированию поперечных несимметричных режимов в ПК RastrWin. Такие модели необходимы для расчётов дуговых коротких замыканий.
Содержание
Оценка сопротивления дуги
По расчётным данным металлического короткого замыкания можно оценить сопротивление дуги с учётом того, что:
- Есть только периодическая составляющая тока короткого замыкания.
- Сопротивление дуги с течением времени постоянно.
- ЭДС совпадает по направлению с осью действительных чисел.
Для каждого вида короткого замыкания можно вывести уравнение для оценки сопротивления дуги.
Пусть дуга это три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный [math]I_a[/math] по модулю.
Неизвестные: [math]R_a, I_a[/math]
Обозначения: $$ \dot{I}_a = I_a \cdot \left(\cos(\varphi) + j \cdot \sin(\varphi) \right), $$
$$ \dot{E} = E, $$
$$ \dot{Z}_0 = R_0 + j \cdot X_0, $$
$$ \dot{Z}_1 = R_1 + j \cdot X_1, $$
$$ \dot{Z}_2 = R_2 + j \cdot X_2. $$
Короткие замыкания на землю
Трехфазное КЗ
Система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = \dot{I}_a \cdot (R_a + \dot{Z}_1), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$
- Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:
$$ K = U \cdot L $$ $$ B = 1 $$ $$ R^\prime = R_1 $$ $$ X^\prime = X_1 $$
Однофазное КЗ
Система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = \frac{1}{3} \cdot \dot{I}_a \cdot (R_a + \dot{Z}_0 + \dot{Z}_1 + \dot{Z}_2), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$
- Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:
$$ K = U \cdot L $$ $$ B = \frac{1}{3} $$ $$ R^\prime = R_0 + R_1 + R_2 $$ $$ X^\prime = X_0 + X_1 + X_2 $$
Двухфазное КЗ на землю
Система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = - \frac{1}{3} \cdot \dot{I}_a \cdot \left(2 \cdot R_a + \dot{Z}_0 + \dot{Z}_1 + \frac{\dot{Z}_0 \cdot \dot{Z}_1}{\dot{Z}_2}\right), \\ 2 \cdot R_a = \frac{2 \cdot U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$
- Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:
$$ K = 2 \cdot U \cdot L $$ $$ B = - \frac{1}{3} $$ $$ R^\prime = R_0 + R_1 + \frac{R_0 R_1 R_2 - X_0 X_1 R_2 + R_0 X_1 X_2 + X_0 R_1 X_2}{R_2^{2} + X_2^{2}} $$ $$ X^\prime = X_0 + X_1 + \frac{R_0 X_1 R_2 + X_0 R_1 R_2 - R_0 R_1 X_2 + X_0 X_1 X_2}{R_2^{2} + X_2^{2}} $$
Общая часть
Общая система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = B \cdot \dot{I}_a \cdot (R_a + R^\prime + j \cdot X^\prime), \\ R_a = \frac{K}{I_a} \end{array}\right. $$
Решение:
$$ E = B \cdot I_a \cdot \left(\cos(\varphi) + j \cdot \sin(\varphi) \right) \cdot \left(\frac{K}{I_a} + R^\prime + j \cdot X^\prime \right) $$
- Внесём [math]I_a[/math] в скобки и разделим обе части на [math](\cos(\varphi) + j \cdot \sin(\varphi))[/math]:
$$ \frac{E}{\cos(\varphi) + j \cdot \sin(\varphi)} = B \cdot \left(K + I_a \cdot R^\prime + j \cdot I_a \cdot X^\prime \right) $$
- Преобразуем:
$$ E \cdot (\cos(\varphi) - j \cdot \sin(\varphi)) = B \cdot \left(K + I_a \cdot R^\prime + j \cdot I_a \cdot X^\prime \right) $$
- Раскроем скобки, приравняем действительные и мнимые компоненты:
$$ \left\{\begin{array}{@{}B@{}} \cos(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) , \\ -\sin(\varphi) \cdot E = B \cdot I_a \cdot X^\prime \end{array}\right. $$
- Выразим [math]I_a[/math] из второго уравнения:
$$ I_a = -\sin(\varphi) \cdot \frac{E}{B \cdot X^\prime} $$
- Подставим [math]I_a[/math] в первое уравнение:
$$ \cos(\varphi) \cdot E = B \cdot K - B \cdot \sin(\varphi) \cdot \frac{E \cdot R^\prime}{B \cdot X^\prime} $$
- Домножим на [math]X^\prime[/math], приведем подобные:
$$ \cos(\varphi) \cdot E \cdot X^\prime = B \cdot K \cdot X^\prime - \sin(\varphi) \cdot E \cdot R^\prime $$
$$ \cos(\varphi) \cdot E \cdot X^\prime + \sin(\varphi) \cdot E \cdot R^\prime = B \cdot K \cdot X^\prime $$
- Введем переменные:
$$ A = \sqrt{(E \cdot X^\prime)^2 + (E \cdot R^\prime)^2} $$
$$ \alpha = atan2\left( (E \cdot R^\prime), (E \cdot X^\prime) \right) $$
$$ \cos(\alpha) = \frac{E \cdot X^\prime}{A} $$ $$ \sin(\alpha) = \frac{E \cdot R^\prime}{A} $$
- Подставим переменные, разделив уравнение на [math]A[/math]:
$$ \cos(\varphi) \cdot \cos(\alpha) + \sin(\varphi) \cdot \sin(\alpha) = \frac{B \cdot K \cdot X^\prime}{A} $$
- Записанное слева — косинус разности:
$$ \cos(\varphi - \alpha) = \frac{B \cdot K \cdot X^\prime}{A} $$
- Решим относительно [math]\varphi[/math]:
$$ \varphi = \alpha \pm acos \left( \frac{B \cdot K \cdot X^\prime}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$
- [math]I_a[/math] находится из первого уравнения системы:
$$ \left\{\begin{array}{@{}B@{}} \cos(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) , \\ -\sin(\varphi) \cdot E = B \cdot I_a \cdot X^\prime \end{array}\right. $$
- И подставляется в выражение:
$$ R_a = \frac{K}{I_a} $$
Короткие замыкания без земли
Двухфазное КЗ
Система для решения:
$$ \left\{ \begin{array}{@{}l@{}} \dot{E} = j\frac{1}{\sqrt{3}} \cdot \dot{I}_a \cdot (\frac{R_a}{2} + \dot{Z}_1 + \dot{Z}_2), \\ \frac{R_a}{2} = \frac{U \cdot L}{2 \cdot I_a} = \frac{K}{I_a} \end{array}\right. $$
- Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:
$$ K =\frac{U \cdot L}{2} $$ $$ B =\frac{1}{\sqrt{3}} $$ $$ R^\prime = R_1 + R_2 $$ $$ X^\prime = X_1 + X_2 $$
Решение:
$$ E = j\cdot B \cdot I_a \cdot \left(\cos(\varphi) + j \cdot \sin(\varphi) \right) \cdot \left(\frac{K}{I_a} + R^\prime + j \cdot X^\prime \right) $$
- Внесём [math]I_a[/math] в скобки и разделим обе части на [math](\cos(\varphi) + j \cdot \sin(\varphi))[/math]:
$$ \frac{E}{\cos(\varphi) + j \cdot \sin(\varphi)} = j \cdot B \cdot \left(K + I_a \cdot R^\prime + j \cdot I_a \cdot X^\prime \right) $$
- Преобразуем:
$$ E \cdot (\cos(\varphi) - j \cdot \sin(\varphi)) = j \cdot B \cdot (K + I_a \cdot R^\prime) - B \cdot I_a \cdot X^\prime $$
- Раскроем скобки, приравняем действительные и мнимые компоненты:
$$ \left\{\begin{array}{@{}l@{}} \cos(\varphi) \cdot E = - B \cdot I_a \cdot X^\prime, \\ -\sin(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) \end{array}\right. $$
- Выразим [math]I_a[/math] из первого уравнения:
$$ I_a = - \cos(\varphi) \cdot \frac{E}{B \cdot X^\prime} $$
- Подставим [math]I_a[/math] во второе уравнение:
$$ -\sin(\varphi) \cdot E = B \cdot K - B \cdot \cos(\varphi) \cdot \frac{E \cdot R^\prime}{B \cdot X^\prime} $$
- Домножим на [math]X^\prime[/math], приведем подобные:
$$ -\sin(\varphi) \cdot E \cdot X^\prime = B \cdot K \cdot X^\prime - \cos(\varphi) \cdot E \cdot R^\prime $$
$$ \cos(\varphi) \cdot E \cdot R^\prime - \sin(\varphi) \cdot E \cdot X^\prime = B \cdot K \cdot X^\prime $$
- Введем переменные:
$$ A = \sqrt{(E \cdot R^\prime)^2 + (E \cdot X^\prime)^2} $$
$$ \alpha = atan2\left( (E \cdot X^\prime), (E \cdot R^\prime) \right) $$
$$ \cos(\alpha) = \frac{E \cdot R^\prime}{A} $$ $$ \sin(\alpha) = \frac{E \cdot X^\prime}{A} $$
- Подставим переменные, разделив уравнение на [math]A[/math]:
$$ \cos(\varphi) \cdot \cos(\alpha) - \sin(\varphi) \cdot \sin(\alpha) = \frac{B \cdot K \cdot X^\prime}{A} $$
- Записанное слева — косинус разности:
$$ \cos(\varphi + \alpha) = \frac{B \cdot K \cdot X^\prime}{A} $$
- Решим относительно [math]\varphi[/math]:
$$ \varphi = - \alpha \pm acos \left( \frac{B \cdot K \cdot X^\prime}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$
- [math]I_a[/math] находится из второго уравнения системы:
$$ \left\{\begin{array}{@{}l@{}} \cos(\varphi) \cdot E = - B \cdot I_a \cdot X^\prime, \\ -\sin(\varphi) \cdot E = B \cdot \left(K + I_a \cdot R^\prime \right) \end{array}\right. $$
- И подставляется в выражение:
$$ R_a = \frac{K}{I_a} $$