Моделирование дуговых поперечных несимметричных режимов в RastrWin

В статье описан подход к моделированию поперечных несимметричных режимов в ПК RastrWin. Такие модели необходимы для расчётов дуговых коротких замыканий.

Оценка сопротивления дуги

По расчётным данным металлического короткого замыкания можно оценить сопротивление дуги с учётом того, что:

• Есть только переодическая состовляющая тока короткого замыкания.
• Сопротивление дуги с течением времени постоянно.

Для каждого вида короткого замыкания можно вывести уравнение для оценки сопротивления дуги.

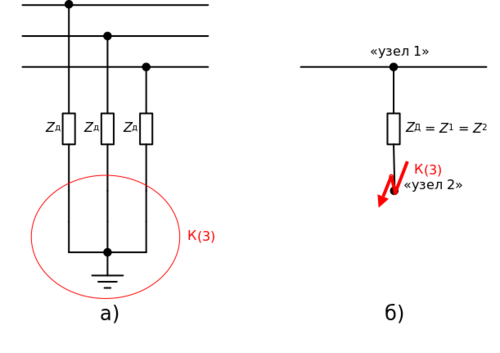
Трёхфазные замыкания

Рисунок 1. Моделирование поперечной несимметрии при К(3).

Пусть дуга это просто три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный [math]I_a[/math] по модулю.

Обозначения: $$ \dot{I}_a = I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right), $$

$$ \dot{E} = E^\prime + j \cdot E^{\prime\prime} $$

$$ \dot{Z}_1 = R_1 + j \cdot X_1 $$

1. Система для решения:

$$ \left\{ \begin{array}{@{}l@{}} \dot{E} = \dot{I}_a \cdot (R_a + \dot{Z}_1), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

2. Неизвестные: [math]R_a, I_a[/math]

3. Решение:

• Подставим [math]R_a[/math] из второго уравнения в первое

$$ \dot{E} = \dot{I}_a \cdot \left(\frac{K}{I_a} + \dot{Z}_1 \right) $$

• Подставим величины из обозначений:

$$ E^\prime + j \cdot E^{\prime\prime} = I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right) \cdot \left(\frac{K}{I_a} + R_1 + j \cdot X_1 \right) $$

• Раскроем скобки, приравняем действительные и мнимые компоненты:

$$ \left\{\begin{array}{@{}l@{}} E^\prime = I_a \cdot \left(\cos(\psi) \cdot (\frac{K}{I_a} + R_1) - \sin(\psi) \cdot X_1 \right), \\ E^{\prime\prime} = I_a \cdot \left(\sin(\psi) \cdot (\frac{K}{I_a} + R_1) + \cos(\psi) \cdot X_1 \right) \end{array}\right. $$

• Раскроем оставшиеся скобки:

$$ \left\{\begin{array}{@{}l@{}} E^\prime = \cos(\psi) \cdot (K + I_a \cdot R_1) - \sin(\psi) \cdot I_a \cdot X_1 , \\ E^{\prime\prime} = \sin(\psi) \cdot (K + I_a \cdot R_1) + \cos(\psi) \cdot I_a \cdot X_1 \end{array}\right. $$

• Перепишем в виде СЛУ:

$$ \begin{bmatrix} E^\prime \\ E^{\prime\prime} \\ \end{bmatrix} = \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} K + I_a \cdot R_1 \\ I_a \cdot X_1 \\ \end{bmatrix} $$

• Заметим ортогональную матрицу (можно было сделать еще в комплексной форме):

$$ \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} ^{-1} = \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} $$

• Решение системы:

$$ \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} E^{\prime} \\ E^{\prime\prime} \\ \end{bmatrix} = \begin{bmatrix} K + I_a \cdot R_1 \\ I_a \cdot X_1 \\ \end{bmatrix} $$

• Запишем в виде системы:

$$ \left\{\begin{array}{@{}l@{}} \cos(\psi) \cdot E^\prime + \sin(\psi) \cdot E^{\prime\prime} = K + I_a \cdot R_1 , \\ -\sin(\psi) \cdot E^\prime + \cos(\psi) \cdot E^{\prime\prime} = I_a \cdot X_1 \end{array}\right. $$

• Выразим [math]I_a[/math] из второго уравнения:

$$ I_a = -\sin(\psi) \cdot \frac{E^\prime}{X_1} + \cos(\psi) \cdot \frac{E^{\prime\prime}}{X_1} $$

• Подставим [math]I_a[/math] в первое уравнение:

$$ \cos(\psi) \cdot E^\prime + \sin(\psi) \cdot E^{\prime\prime} = K - \sin(\psi) \cdot \frac{E^\prime \cdot R_1}{X_1} + \cos(\psi) \cdot \frac{E^{\prime\prime} \cdot R_1}{X_1} $$

• Домножим на [math]X_1[/math], приведем подобные:

$$ \cos(\psi) \cdot E^\prime \cdot X_1 + \sin(\psi) \cdot E^{\prime\prime} \cdot X_1 = K \cdot X_1 - \sin(\psi) \cdot E^\prime \cdot R_1 + \cos(\psi) \cdot E^{\prime\prime} \cdot R_1 $$

$$ \cos(\psi) \cdot (E^\prime \cdot X_1 - E^{\prime\prime} \cdot R_1) + \sin(\psi) \cdot (E^{\prime\prime} \cdot X_1 + E^\prime \cdot R_1) = K \cdot X_1 $$

• Введем переменные:

$$ A = \sqrt{(E^\prime \cdot X_1 - E^{\prime\prime} \cdot R_1)^2 + (E^{\prime\prime} \cdot X_1 + E^\prime \cdot R_1)^2} = \sqrt{(E^\prime \cdot X_1)^2 + (E^{\prime\prime} \cdot R_1)^2 + (E^{\prime\prime} \cdot X_1)^2 + (E^\prime \cdot R_1)^2} $$

$$ \alpha = atan2\left( (E^\prime \cdot X_1 - E^{\prime\prime} \cdot R_1), (E^{\prime\prime} \cdot X_1 + E^\prime \cdot R_1) \right) $$

$$ \cos(\alpha) = \frac{E^\prime \cdot X_1 - E^{\prime\prime} \cdot R_1}{A} $$ $$ \sin(\alpha) = \frac{E^{\prime\prime} \cdot X_1 + E^\prime \cdot R_1}{A} $$

• Подставим переменные, разделив уравнение на [math]A[/math]:

$$ \cos(\psi) \cdot \cos(\alpha) + \sin(\psi) \cdot \sin(\alpha) = \frac{K \cdot X_1}{A} $$

• Записанное слева — косинус разности:

$$ \cos(\psi - \alpha) = \frac{K \cdot X_1}{A} $$

• Решим относительно [math]\psi[/math]:

$$ \psi = \alpha \pm acos \left( \frac{K \cdot X_1}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$

• [math]I_a[/math] находится из первого уравнения системы 7.

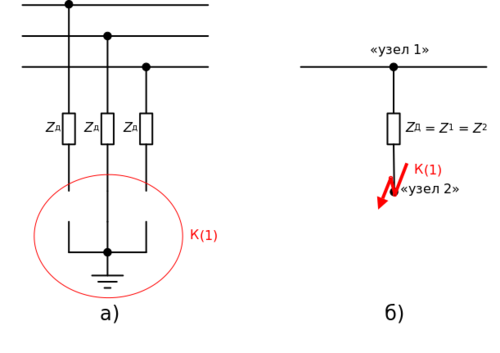
Однофазные замыкания

Рисунок 2. Моделирование поперечной несимметрии при К(1).

Пусть дуга это три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный [math]I_a[/math] по модулю.

Обозначения: $$ \dot{I}_a = I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right), $$

$$ \dot{E} = E^\prime + j \cdot E^{\prime\prime} $$

$$ \dot{Z}_0 = R_0 + j \cdot X_0 $$

$$ \dot{Z}_1 = R_1 + j \cdot X_1 $$

$$ \dot{Z}_2 = R_2 + j \cdot X_2 $$

1. Система для решения:

$$ \left\{ \begin{array}{@{}l@{}} \dot{E} = \frac{1}{3} \cdot \dot{I}_a \cdot (R_a + \dot{Z}_0 + \dot{Z}_1 + \dot{Z}_2), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

2. Неизвестные: [math]R_a, I_a[/math]

3. Решение:

• Подставим [math]R_a[/math] из второго уравнения в первое

$$ \dot{E} = \frac{1}{3} \cdot \dot{I}_a \cdot \left(\frac{K}{I_a} + \dot{Z}_0 + \dot{Z}_1 + \dot{Z}_2\right) $$

• Подставим величины из обозначений:

$$ E^\prime + j \cdot E^{\prime\prime} = \frac{1}{3} \cdot I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right) \cdot \left(\frac{K}{I_a} + R_0 + j \cdot X_0 + R_1 + j \cdot X_1 + R_2 + j \cdot X_2 \right) $$

• Раскроем скобки, приравняем действительные и мнимые компоненты:

$$ \left\{\begin{array}{@{}l@{}} E^\prime = \frac{1}{3} I_a \cdot \left(\cos(\psi) \cdot (\frac{K}{I_a} + R_0 + R_1 + R_2) - \sin(\psi) \cdot (X_0 + X_1 + X_2) \right), \\ E^{\prime\prime} = \frac{1}{3} I_a \cdot \left(\sin(\psi) \cdot (\frac{K}{I_a} + R_0 + R_1 + R_2) + \cos(\psi) \cdot (X_0 + X_1 + X_2) \right) \end{array}\right. $$

• Раскроем оставшиеся скобки:

$$ \left\{\begin{array}{@{}l@{}} 3 \cdot E^\prime = \cos(\psi) \cdot (K + I_a \cdot (R_0 + R_1 + R_2)) - \sin(\psi) \cdot I_a \cdot (X_0 + X_1 + X_2) , \\ 3 \cdot E^{\prime\prime} = \sin(\psi) \cdot (K + I_a \cdot (R_0 + R_1 + R_2)) + \cos(\psi) \cdot I_a \cdot (X_0 + X_1 + X_2) \end{array}\right. $$

• Перепишем в виде СЛУ:

$$ \begin{bmatrix} E^\prime \\ E^{\prime\prime} \\ \end{bmatrix} = \frac{1}{3} \cdot \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} K + I_a \cdot (R_0 + R_1 + R_2) \\ I_a \cdot (X_0 + X_1 + X_2) \\ \end{bmatrix} $$

• Заметим ортогональную матрицу (можно было сделать еще в комплексной форме):

$$ \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} ^{-1} = \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} $$

• Решение системы:

$$ \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} E^{\prime} \\ E^{\prime\prime} \\ \end{bmatrix} = \frac{1}{3} \cdot \begin{bmatrix} K + I_a \cdot (R_0 + R_1 + R_2) \\ I_a \cdot (X_0 + X_1 + X_2) \\ \end{bmatrix} $$

• Запишем в виде системы:

$$ \left\{\begin{array}{@{}l@{}} \cos(\psi) \cdot E^\prime + \sin(\psi) \cdot E^{\prime\prime} = \frac{1}{3} \left(K + I_a \cdot (R_0 + R_1 + R_2)\right) , \\ -\sin(\psi) \cdot E^\prime + \cos(\psi) \cdot E^{\prime\prime} = \frac{1}{3} I_a \cdot (X_0 + X_1 + X_2) \end{array}\right. $$

• Выразим [math]I_a[/math] из второго уравнения:

$$ I_a = -\sin(\psi) \cdot \frac{3 E^\prime}{X_0 + X_1 + X_2} + \cos(\psi) \cdot \frac{3 E^{\prime\prime}}{X_0 + X_1 + X_2} $$

• Подставим [math]I_a[/math] в первое уравнение:

$$ \cos(\psi) \cdot 3 E^\prime + \sin(\psi) \cdot 3 E^{\prime\prime} = K - \sin(\psi) \cdot \frac{3 E^\prime \cdot (R_0 + R_1 + R_2)}{X_0 + X_1 + X_2} + \cos(\psi) \cdot \frac{3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2)}{X_0 + X_1 + X_2} $$

• Домножим на [math]X_0 + X_1 + X_2[/math], приведем подобные:

$$ \cos(\psi) \cdot 3 E^\prime \cdot (X_0 + X_1 + X_2) + \sin(\psi) \cdot 3 E^{\prime\prime} \cdot (X_0 + X_1 + X_2) = K \cdot (X_0 + X_1 + X_2) - \sin(\psi) \cdot 3 E^\prime \cdot (R_0 + R_1 + R_2) + \cos(\psi) \cdot 3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2) $$

$$ \cos(\psi) \cdot (3 E^\prime \cdot (X_0 + X_1 + X_2) - 3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2)) + \sin(\psi) \cdot (3 E^{\prime\prime} \cdot (X_0 + X_1 + X_2) + 3 E^\prime \cdot (R_0 + R_1 + R_2)) = K \cdot (X_0 + X_1 + X_2) $$

• Введем переменные:

$$ A = \sqrt{(3 E^\prime \cdot (X_0 + X_1 + X_2) - 3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2))^2 + (3 E^{\prime\prime} \cdot (X_0 + X_1 + X_2) + 3 E^\prime \cdot (R_0 + R_1 + R_2))^2} = \sqrt{(3 E^\prime \cdot (X_0 + X_1 + X_2))^2 + (3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2))^2 + (3 E^{\prime\prime} \cdot (X_0 + X_1 + X_2))^2 + (3 E^\prime \cdot (R_0 + R_1 + R_2))^2} $$

$$ \alpha = atan2\left( (3 E^\prime \cdot (X_0 + X_1 + X_2) - 3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2)), (3 E^{\prime\prime} \cdot (X_0 + X_1 + X_2) + 3 E^\prime \cdot (R_0 + R_1 + R_2)) \right) $$

$$ \cos(\alpha) = \frac{3 E^\prime \cdot (X_0 + X_1 + X_2) - 3 E^{\prime\prime} \cdot (R_0 + R_1 + R_2)}{A} $$ $$ \sin(\alpha) = \frac{3 E^{\prime\prime} \cdot (X_0 + X_1 + X_2) + 3 E^\prime \cdot (R_0 + R_1 + R_2)}{A} $$

• Подставим переменные, разделив уравнение на [math]A[/math]:

$$ \cos(\psi) \cdot \cos(\alpha) + \sin(\psi) \cdot \sin(\alpha) = \frac{K \cdot (X_0 + X_1 + X_2)}{A} $$

• Записанное слева — косинус разности:

$$ \cos(\psi - \alpha) = \frac{K \cdot (X_0 + X_1 + X_2)}{A} $$

• Решим относительно [math]\psi[/math]:

$$ \psi = \alpha \pm acos \left( \frac{K \cdot (X_0 + X_1 + X_2)}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$

• [math]I_a[/math] находится из первого уравнения системы 7.

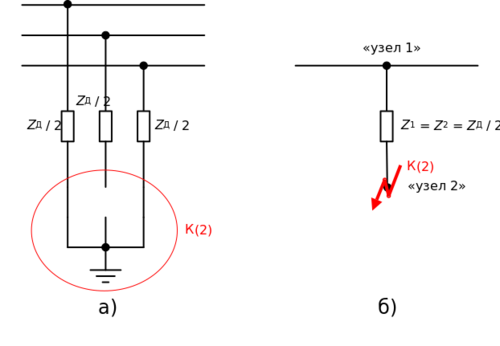
Двухфазные замыкания без земли

Рисунок 3. Моделирование поперечной несимметрии при К(2).

Пусть дуга это три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный [math]I_a[/math] по модулю.

Обозначения: $$ \dot{I}_a = I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right), $$

$$ \dot{E} = E^\prime + j \cdot E^{\prime\prime} $$

$$ \dot{Z}_1 = R_1 + j \cdot X_1 $$

$$ \dot{Z}_2 = R_2 + j \cdot X_2 $$

1. Система для решения:

$$ \left\{ \begin{array}{@{}l@{}} \dot{E} = j\frac{1}{\sqrt{3}} \cdot \dot{I}_a \cdot (R_a + \dot{Z}_1 + \dot{Z}_2), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

2. Неизвестные: [math]R_a, I_a[/math]

3. Решение:

• Подставим [math]R_a[/math] из второго уравнения в первое

$$ \dot{E} = j\frac{1}{\sqrt{3}} \cdot \dot{I}_a \cdot \left(\frac{K}{I_a} + \dot{Z}_1 + \dot{Z}_2 \right) $$

• Подставим величины из обозначений:

$$ E^\prime + j \cdot E^{\prime\prime} = j\frac{1}{\sqrt{3}} \cdot I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right) \cdot \left(\frac{K}{I_a} + R_1 + j \cdot X_1 + R_2 + j \cdot X_2 \right) $$

• Раскроем скобки, приравняем действительные и мнимые компоненты:

$$ \left\{\begin{array}{@{}l@{}} E^\prime = \frac{1}{\sqrt{3}} I_a \cdot \left( - \sin(\psi) \cdot (\frac{K}{I_a} + R_1 + R_2) - \cos(\psi) \cdot (X_1 + X_2) \right), \\ E^{\prime\prime} = \frac{1}{\sqrt{3}} I_a \cdot \left(\cos(\psi) \cdot (\frac{K}{I_a} + R_1 + R_2) - \sin(\psi) \cdot (X_1 + X_2) \right) \end{array}\right. $$

• Раскроем оставшиеся скобки:

$$ \left\{\begin{array}{@{}l@{}} \sqrt{3} \cdot E^\prime = - \sin(\psi) \cdot (K + I_a \cdot (R_1 + R_2)) - \cos(\psi) \cdot I_a \cdot (X_1 + X_2) , \\ \sqrt{3} \cdot E^{\prime\prime} = \cos(\psi) \cdot (K + I_a \cdot (R_1 + R_2)) - \sin(\psi) \cdot I_a \cdot (X_1 + X_2) \end{array}\right. $$

• Перепишем в виде СЛУ:

$$ \begin{bmatrix} E^\prime \\ E^{\prime\prime} \\ \end{bmatrix} = \frac{1}{\sqrt{3}} \cdot \begin{bmatrix} -\sin(\psi) & - \cos(\psi) \\ \cos(\psi) & - \sin(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} K + I_a \cdot (R_1 + R_2) \\ I_a \cdot (X_1 + X_2) \\ \end{bmatrix} $$

• Заметим ортогональную матрицу (можно было сделать еще в комплексной форме):

$$ \begin{bmatrix} -\sin(\psi) & - \cos(\psi) \\ \cos(\psi) & - \sin(\psi) \\ \end{bmatrix} ^{-1} = \begin{bmatrix} -\sin(\psi) & \cos(\psi) \\ -\cos(\psi) & - \sin(\psi) \\ \end{bmatrix} $$

• Решение системы:

$$ \begin{bmatrix} -\sin(\psi) & \cos(\psi) \\ -\cos(\psi) & - \sin(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} E^{\prime} \\ E^{\prime\prime} \\ \end{bmatrix} = \frac{1}{\sqrt{3}} \cdot \begin{bmatrix} K + I_a \cdot (R_1 + R_2) \\ I_a \cdot (X_1 + X_2) \\ \end{bmatrix} $$

• Запишем в виде системы:

$$ \left\{\begin{array}{@{}l@{}} -\sin(\psi) \cdot \sqrt{3} E^\prime + \cos(\psi) \cdot \sqrt{3} E^{\prime\prime} = K + I_a \cdot (R_1 + R_2) , \\ -\cos(\psi) \cdot \sqrt{3} E^\prime - \sin(\psi) \cdot \sqrt{3} E^{\prime\prime} = I_a \cdot (X_1 + X_2) \end{array}\right. $$

• Выразим [math]I_a[/math] из второго уравнения:

$$ I_a = -\cos(\psi) \cdot \frac{\sqrt{3} E^\prime}{(X_1 + X_2)} - \sin(\psi) \cdot \frac{\sqrt{3} E^{\prime\prime}}{(X_1 + X_2)} $$

• Подставим [math]I_a[/math] в первое уравнение:

$$ -\sin(\psi) \cdot \sqrt{3} E^\prime + \cos(\psi) \cdot \sqrt{3} E^{\prime\prime} = K - \cos(\psi) \cdot \frac{\sqrt{3} E^\prime \cdot (R_1 + R_2)}{X_1 + X_2} - \sin(\psi) \cdot \frac{\sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2)}{X_1 + X_2} $$

• Домножим на [math]X_1 + X_2[/math], приведем подобные:

$$ -\sin(\psi) \cdot \sqrt{3} E^\prime \cdot (X_1 + X_2) + \cos(\psi) \cdot \sqrt{3} E^{\prime\prime} \cdot (X_1 + X_2) = K \cdot (X_1 + X_2) - \cos(\psi) \cdot \sqrt{3} E^\prime \cdot (R_1 + R_2) - \sin(\psi) \cdot \sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2) $$

$$ \cos(\psi) \cdot (\sqrt{3} E^\prime \cdot (R_1 + R_2) + \sqrt{3} E^{\prime\prime} \cdot (X_1 + X_2)) + \sin(\psi) \cdot (\sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2) - \sqrt{3} E^\prime \cdot (X_1 + X_2)) = K \cdot (X_1 + X_2) $$

• Введем переменные:

$$ A = \sqrt{(\sqrt{3} E^\prime \cdot (R_1 + R_2) + \sqrt{3} E^{\prime\prime} \cdot (X_1 + X_2))^2 + (\sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2) - \sqrt{3} E^\prime \cdot (X_1 + X_2))^2} = \sqrt{(\sqrt{3} E^\prime \cdot (R_1 + R_2))^2 + (\sqrt{3} E^{\prime\prime} \cdot (X_1 + X_2))^2 + (\sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2))^2 + (\sqrt{3} E^\prime \cdot (X_1 + X_2))^2} $$

$$ \alpha = atan2\left( (\sqrt{3} E^\prime \cdot (R_1 + R_2) + \sqrt{3} E^{\prime\prime} \cdot (X_1 + X_2)), (\sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2) - \sqrt{3} E^\prime \cdot (X_1 + X_2)) \right) $$

$$ \cos(\alpha) = \frac{\sqrt{3} E^\prime \cdot (R_1 + R_2) + \sqrt{3} E^{\prime\prime} \cdot (X_1 + X_2)}{A} $$ $$ \sin(\alpha) = \frac{\sqrt{3} E^{\prime\prime} \cdot (R_1 + R_2) - \sqrt{3} E^\prime \cdot (X_1 + X_2)}{A} $$

• Подставим переменные, разделив уравнение на [math]A[/math]:

$$ \cos(\psi) \cdot \cos(\alpha) + \sin(\psi) \cdot \sin(\alpha) = \frac{K \cdot (X_1 + X_2)}{A} $$

• Записанное слева — косинус разности:

$$ \cos(\psi - \alpha) = \frac{K \cdot (X_1 + X_2)}{A} $$

• Решим относительно [math]\psi[/math]:

$$ \psi = \alpha \pm acos \left( \frac{K \cdot (X_1 + X_2)}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$

• [math]I_a[/math] находится из первого уравнения системы 7.

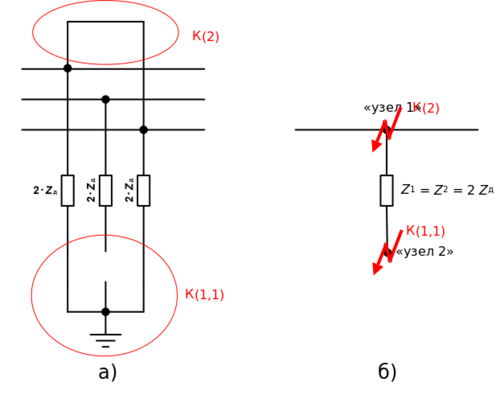
Двухфазные замыкания на землю

Рисунок 4. Моделирование поперечной несимметрии при К(1,1).

Пусть дуга это три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный [math]I_a[/math] по модулю.

Обозначения: $$ \dot{I}_a = I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right), $$

$$ \dot{E} = E^\prime + j \cdot E^{\prime\prime} $$

$$ \dot{Z}_0 = R_0 + j \cdot X_0 $$

$$ \dot{Z}_1 = R_1 + j \cdot X_1 $$

$$ \dot{Z}_2 = R_2 + j \cdot X_2 $$

1. Система для решения:

$$ \left\{ \begin{array}{@{}l@{}} \dot{E} = - \frac{1}{3} \cdot \dot{I}_a \cdot \left(R_a + \dot{Z}_0 + \dot{Z}_1 + \frac{\dot{Z}_0 \cdot \dot{Z}_1}{\dot{Z}_2}\right), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

2. Неизвестные: [math]R_a, I_a[/math]

3. Решение:

• Подставим [math]R_a[/math] из второго уравнения в первое

$$ \dot{E} = - \frac{1}{3} \cdot \dot{I}_a \cdot \left(\frac{K}{I_a} + \dot{Z}_0 + \dot{Z}_1 + \frac{\dot{Z}_0 \cdot \dot{Z}_1}{\dot{Z}_2}\right) $$

• Подставим величины из обозначений:

$$ E^\prime + j \cdot E^{\prime\prime} = - \frac{1}{3} \cdot I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right) \cdot \left(\frac{K}{I_a} + R_0 + j \cdot X_0 + R_1 + j \cdot X_1 +\frac{(R_0 + j \cdot X_0) \cdot (R_1 + j \cdot X_1)}{R_2 + j \cdot X_2} \right) $$

• Раскроем скобки, разделим действительную и мнимую составляющие сопротивлений, связанных с симметричными составляющими:

$$ R^\prime + j \cdot X^\prime = R_0 + j \cdot X_0 + R_1 + j \cdot X_1 +\frac{(R_0 + j \cdot X_0) \cdot (R_1 + j \cdot X_1)}{R_2 + j \cdot X_2} $$

$$ R^\prime = R_0 + R_1 + \frac{R_0 R_1 R_2 - X_0 X_1 R_2 + R_0 X_1 X_2 + X_0 R_1 X_2}{R_2^{2} + X_2^{2}} $$

$$ X^\prime = X_0 + X_1 + \frac{R_0 X_1 R_2 + X_0 R_1 R_2 - R_0 R_1 X_2 + X_0 X_1 X_2}{R_2^{2} + X_2^{2}} $$

$$ E^\prime + j \cdot E^{\prime\prime} = - \frac{1}{3} \cdot I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right) \cdot \left(\frac{K}{I_a} + R^\prime + j \cdot X^\prime \right) $$

• Раскроем скобки, приравняем действительные и мнимые компоненты:

$$ \left\{\begin{array}{@{}l@{}} E^\prime = - \frac{1}{3} I_a \cdot \left(\cos(\psi) \cdot (\frac{K}{I_a} + R^\prime) - \sin(\psi) \cdot X^\prime \right), \\ E^{\prime\prime} = - \frac{1}{3} I_a \cdot \left(\sin(\psi) \cdot (\frac{K}{I_a} + R^\prime) + \cos(\psi) \cdot X^\prime \right) \end{array}\right. $$

• Раскроем оставшиеся скобки:

$$ \left\{\begin{array}{@{}l@{}} -3 \cdot E^\prime = \cos(\psi) \cdot (K + I_a \cdot R^\prime) - \sin(\psi) \cdot I_a \cdot X^\prime , \\ -3 \cdot E^{\prime\prime} = \sin(\psi) \cdot (K + I_a \cdot R^\prime) + \cos(\psi) \cdot I_a \cdot X^\prime \end{array}\right. $$

• Перепишем в виде СЛУ:

$$ \begin{bmatrix} E^\prime \\ E^{\prime\prime} \\ \end{bmatrix} = - \frac{1}{3} \cdot \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} K + I_a \cdot R^\prime \\ I_a \cdot X^\prime \\ \end{bmatrix} $$

• Заметим ортогональную матрицу (можно было сделать еще в комплексной форме):

$$ \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} ^{-1} = \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} $$

• Решение системы:

$$ \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} E^{\prime} \\ E^{\prime\prime} \\ \end{bmatrix} = - \frac{1}{3} \cdot \begin{bmatrix} K + I_a \cdot R^\prime \\ I_a \cdot X^\prime \\ \end{bmatrix} $$

• Запишем в виде системы:

$$ \left\{\begin{array}{@{}l@{}} \cos(\psi) \cdot E^\prime + \sin(\psi) \cdot E^{\prime\prime} = - \frac{1}{3} \left(K + I_a \cdot R^\prime \right) , \\ -\sin(\psi) \cdot E^\prime + \cos(\psi) \cdot E^{\prime\prime} = - \frac{1}{3} I_a \cdot X^\prime \end{array}\right. $$

• Выразим [math]I_a[/math] из второго уравнения:

$$ I_a = \sin(\psi) \cdot \frac{3 E^\prime}{X^\prime} - \cos(\psi) \cdot \frac{3 E^{\prime\prime}}{X^\prime} $$

• Подставим [math]I_a[/math] в первое уравнение:

$$ - \cos(\psi) \cdot 3 E^\prime - \sin(\psi) \cdot 3 E^{\prime\prime} = K + \sin(\psi) \cdot \frac{3 E^\prime \cdot R^\prime}{X^\prime} - \cos(\psi) \cdot \frac{3 E^{\prime\prime} \cdot R^\prime}{X^\prime} $$

• Домножим на [math]X^\prime[/math], приведем подобные:

$$ -\cos(\psi) \cdot 3 E^\prime \cdot X^\prime - \sin(\psi) \cdot 3 E^{\prime\prime} \cdot X^\prime = K \cdot X^\prime + \sin(\psi) \cdot 3 E^\prime \cdot R^\prime - \cos(\psi) \cdot 3 E^{\prime\prime} \cdot R^\prime $$

$$ \cos(\psi) \cdot (3 E^\prime \cdot X^\prime - 3 E^{\prime\prime} \cdot R^\prime) + \sin(\psi) \cdot (3 E^{\prime\prime} \cdot X^\prime + 3 E^\prime \cdot R^\prime) = - K \cdot X^\prime $$

• Введем переменные:

$$ A = \sqrt{(3 E^\prime \cdot X^\prime - 3 E^{\prime\prime} \cdot R^\prime)^2 + (3 E^{\prime\prime} \cdot X^\prime + 3 E^\prime \cdot R^\prime)^2} = \sqrt{(3 E^\prime \cdot X^\prime)^2 + (3 E^{\prime\prime} \cdot R^\prime)^2 + (3 E^{\prime\prime} \cdot X^\prime)^2 + (3 E^\prime \cdot R^\prime)^2} $$

$$ \alpha = atan2\left( (3 E^\prime \cdot X^\prime - 3 E^{\prime\prime} \cdot R^\prime), (3 E^{\prime\prime} \cdot X^\prime + 3 E^\prime \cdot R^\prime) \right) $$

$$ \cos(\alpha) = \frac{3 E^\prime \cdot X^\prime - 3 E^{\prime\prime} \cdot R^\prime}{A} $$ $$ \sin(\alpha) = \frac{3 E^{\prime\prime} \cdot X^\prime + 3 E^\prime \cdot R^\prime}{A} $$

• Подставим переменные, разделив уравнение на [math]A[/math]:

$$ \cos(\psi) \cdot \cos(\alpha) + \sin(\psi) \cdot \sin(\alpha) = - \frac{K \cdot X^\prime}{A} $$

• Записанное слева — косинус разности:

$$ \cos(\psi - \alpha) = - \frac{K \cdot X^\prime}{A} $$

• Решим относительно [math]\psi[/math]:

$$ \psi = \alpha \pm acos \left( - \frac{K \cdot X^\prime}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$

• [math]I_a[/math] находится из первого уравнения системы 7.

Унификация расчётов для КЗ на землю

Пусть дуга это три одинаковых сопротивления, соединяющих провод, по ней течет ток, равный [math]I_a[/math] по модулю.

Неизвестные: [math]R_a, I_a[/math]

Обозначения: $$ \dot{I}_a = I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right), $$

$$ \dot{E} = E^\prime + j \cdot E^{\prime\prime}, $$

$$ \dot{Z}_0 = R_0 + j \cdot X_0, $$

$$ \dot{Z}_1 = R_1 + j \cdot X_1, $$

$$ \dot{Z}_2 = R_2 + j \cdot X_2. $$

Трехфазное КЗ

Система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = \dot{I}_a \cdot (R_a + \dot{Z}_1), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

• Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:

$$ L = 1 $$ $$ R^\prime = R_1 $$ $$ X^\prime = X_1 $$

Однофазное КЗ

Система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = \frac{1}{3} \cdot \dot{I}_a \cdot (R_a + \dot{Z}_0 + \dot{Z}_1 + \dot{Z}_2), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

• Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:

$$ L = \frac{1}{3} $$ $$ R^\prime = R_0 + R_1 + R_2 $$ $$ X^\prime = X_0 + X_1 + X_2 $$

Двухфазное КЗ на землю

Система для решения: $$ \left\{ \begin{array}{@{}l@{}} \dot{E} = - \frac{1}{3} \cdot \dot{I}_a \cdot \left(R_a + \dot{Z}_0 + \dot{Z}_1 + \frac{\dot{Z}_0 \cdot \dot{Z}_1}{\dot{Z}_2}\right), \\ R_a = \frac{U \cdot L}{I_a} = \frac{K}{I_a} \end{array}\right. $$

• Подставим [math]R_a[/math] из второго уравнения в первое и выполним замену:

$$ L = - \frac{1}{3} $$ $$ R^\prime = R_0 + R_1 + \frac{R_0 R_1 R_2 - X_0 X_1 R_2 + R_0 X_1 X_2 + X_0 R_1 X_2}{R_2^{2} + X_2^{2}} $$ $$ X^\prime = X_0 + X_1 + \frac{R_0 X_1 R_2 + X_0 R_1 R_2 - R_0 R_1 X_2 + X_0 X_1 X_2}{R_2^{2} + X_2^{2}} $$

Общая часть

Решение:

$$ E^\prime + j \cdot E^{\prime\prime} = L \cdot I_a \cdot \left(\cos(\psi) + j \cdot \sin(\psi) \right) \cdot \left(\frac{K}{I_a} + R^\prime + j \cdot X^\prime \right) $$

• Раскроем скобки, приравняем действительные и мнимые компоненты:

$$ \left\{\begin{array}{@{}l@{}} E^\prime = L \cdot I_a \cdot \left(\cos(\psi) \cdot (\frac{K}{I_a} + R^\prime) - \sin(\psi) \cdot X^\prime \right), \\ E^{\prime\prime} = L \cdot I_a \cdot \left(\sin(\psi) \cdot (\frac{K}{I_a} + R^\prime) + \cos(\psi) \cdot X^\prime \right) \end{array}\right. $$

• Внесём [math]I_a[/math] в скобки:

$$ \left\{\begin{array}{@{}l@{}} E^\prime =L \cdot \left( \cos(\psi) \cdot (K + I_a \cdot R^\prime) - \sin(\psi) \cdot I_a \cdot X^\prime \right), \\ E^{\prime\prime} = L \cdot \left( \sin(\psi) \cdot (K + I_a \cdot R^\prime) + \cos(\psi) \cdot I_a \cdot X^\prime\right) \end{array}\right. $$

• Перепишем в виде СЛУ:

$$ \begin{bmatrix} E^\prime \\ E^{\prime\prime} \\ \end{bmatrix} = L \cdot \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} K + I_a \cdot R^\prime \\ I_a \cdot X^\prime \\ \end{bmatrix} $$

• Заметим ортогональную матрицу (можно было сделать еще в комплексной форме):

$$ \begin{bmatrix} \cos(\psi) & - \sin(\psi) \\ \sin(\psi) & \cos(\psi) \\ \end{bmatrix} ^{-1} = \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} $$

• Решение системы:

$$ \begin{bmatrix} \cos(\psi) & \sin(\psi) \\ -\sin(\psi) & \cos(\psi) \\ \end{bmatrix} \cdot \begin{bmatrix} E^{\prime} \\ E^{\prime\prime} \\ \end{bmatrix} = L \cdot \begin{bmatrix} K + I_a \cdot R^\prime \\ I_a \cdot X^\prime \\ \end{bmatrix} $$

• Запишем в виде системы:

$$ \left\{\begin{array}{@{}l@{}} \cos(\psi) \cdot E^\prime + \sin(\psi) \cdot E^{\prime\prime} = L \cdot \left(K + I_a \cdot R^\prime \right) , \\ -\sin(\psi) \cdot E^\prime + \cos(\psi) \cdot E^{\prime\prime} = L \cdot I_a \cdot X^\prime \end{array}\right. $$

• Выразим [math]I_a[/math] из второго уравнения:

$$ I_a = -\sin(\psi) \cdot \frac{E^\prime}{L \cdot X^\prime} + \cos(\psi) \cdot \frac{E^{\prime\prime}}{L \cdot X^\prime} $$

• Подставим [math]I_a[/math] в первое уравнение:

$$ \cos(\psi) \cdot E^\prime + \sin(\psi) \cdot E^{\prime\prime} = L \cdot K - L \cdot \sin(\psi) \cdot \frac{E^\prime \cdot R^\prime}{L \cdot X^\prime} + L \cdot \cos(\psi) \cdot \frac{E^{\prime\prime} \cdot R^\prime}{L \cdot X^\prime} $$

• Домножим на [math]X^\prime[/math], приведем подобные:

$$ \cos(\psi) \cdot E^\prime \cdot X^\prime + \sin(\psi) \cdot E^{\prime\prime} \cdot X^\prime = L \cdot K \cdot X^\prime - \sin(\psi) \cdot E^\prime \cdot R^\prime + \cos(\psi) \cdot E^{\prime\prime} \cdot R^\prime $$

$$ \cos(\psi) \cdot (E^\prime \cdot X^\prime - E^{\prime\prime} \cdot R^\prime) + \sin(\psi) \cdot (E^{\prime\prime} \cdot X^\prime + E^\prime \cdot R^\prime) = L \cdot K \cdot X^\prime $$

• Введем переменные:

$$ A = \sqrt{(E^\prime \cdot X^\prime - E^{\prime\prime} \cdot R^\prime)^2 + (E^{\prime\prime} \cdot X^\prime + E^\prime \cdot R^\prime)^2} = \sqrt{(E^\prime \cdot X^\prime)^2 + (E^{\prime\prime} \cdot R^\prime)^2 + (E^{\prime\prime} \cdot X^\prime)^2 + (E^\prime \cdot R^\prime)^2} $$

$$ \alpha = atan2\left( (E^\prime \cdot X^\prime - E^{\prime\prime} \cdot R^\prime), (E^{\prime\prime} \cdot X^\prime + E^\prime \cdot R^\prime) \right) $$

$$ \cos(\alpha) = \frac{E^\prime \cdot X^\prime - E^{\prime\prime} \cdot R^\prime}{A} $$ $$ \sin(\alpha) = \frac{E^{\prime\prime} \cdot X^\prime + E^\prime \cdot R^\prime}{A} $$

• Подставим переменные, разделив уравнение на [math]A[/math]:

$$ \cos(\psi) \cdot \cos(\alpha) + \sin(\psi) \cdot \sin(\alpha) = \frac{L \cdot K \cdot X^\prime}{A} $$

• Записанное слева — косинус разности:

$$ \cos(\psi - \alpha) = \frac{L \cdot K \cdot X^\prime}{A} $$

• Решим относительно [math]\psi[/math]:

$$ \psi = \alpha \pm acos \left( \frac{L \cdot K \cdot X^\prime}{A} \right) + 2\cdot \pi \cdot k, k \in \mathbb{Z} $$

• [math]I_a[/math] находится из первого уравнения системы 7.