Метод симметричных составляющих

Метод симметричных составляющих — метод расчета несимметричных электричеких систем, основанный на разложении несимметричных систем на три симметричные.

Общие положения

Электрическая система состоит из большого количества элементов. В случае аварии на каком-либо из них, система перестает быть симметричной. Для анализа, зачастую применяют метод симметричных составляющих, суть которого состоит в том, что

Любую несимметричную систему можно однозначно разложить на три симметричные системы: прямой, обратной и нулевой последовательности чередования фаз.

Расчет электрических величин проводят с использованием схем замещения. Комплексные сопротивления для каждой из последовательностей — различны. Поэтому на основании принципа наложения, несимметричный режим представляют как результат наложения трех симметричных режимов. Проводят три расчета для схем замещения прямой, обратной и нулевой последовательности и искомая электрическая величина определяется как сумма составляющих трех последовательностей.

Разложение в комплексных числах

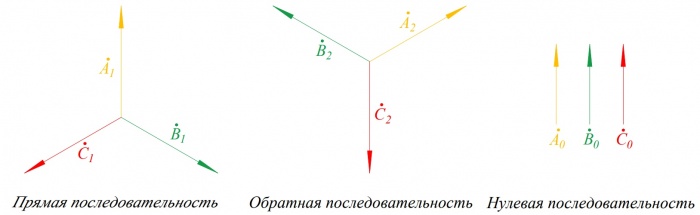
Прямая последовательность

Система прямой последовательности состоит из трех векторов [math]\displaystyle \dot A_{1}, \dot B_{1} \text { и } \dot C_{1} [/math] равных по модулю и повернутых относительно друг друга на угол [math]\displaystyle 120^\circ [/math], причем вектор [math]\displaystyle \dot B_{1}[/math] отстает от вектора [math]\displaystyle \dot A_{1}[/math].

Обратная последовательность

Система обратной последовательности состоит из трех векторов [math]\displaystyle \dot A_{2}, \dot B_{2} \text { и } \dot C_{2} [/math] равных по модулю и повернутых относительно друг друга на угол [math]\displaystyle 120^\circ [/math], причем вектор [math]\displaystyle \dot B_{2}[/math] опережает вектор [math]\displaystyle \dot A_{2}[/math].

Нулевая последовательность

Система нулевой последовательности состоит из трёх векторов [math]\displaystyle \dot A_{0}, \dot B_{0} \text { и } \dot C_{0} [/math] равных по модулю и совпадающих по фазе.

Оператор а

Для упрощения расчетов используется оператор а, который равен:

[math] \displaystyle \dot a=e^{j \cdot 120^\circ}=e^{j \cdot \frac {2 \cdot \pi}{3}} [/math].

Тогда можно записать, что

[math] \displaystyle \dot B_{1} = \dot a^2 \cdot \dot A_{1} \text { и } \dot C_{1} = \dot a \cdot \dot A_{1}[/math];

[math] \displaystyle \dot B_{2} = \dot a \cdot \dot A_{2} \text { и } \dot C_{2} = \dot a^2 \cdot \dot A_{2}[/math];

[math] \displaystyle \dot A_{0} = \dot B_{0} = \dot C_{0}[/math].

Выразим произвольную трехфазную величину [math]\displaystyle \dot A, \dot B \text { и } \dot C [/math] через векторы симметричных составляющих:

[math] \displaystyle \dot A = \dot A_{1} + \dot A_{2} + \dot A_{0}[/math];

[math] \displaystyle \dot B = \dot B_{1} + \dot B_{2} + \dot B_{0}[/math];

[math] \displaystyle \dot C = \dot C_{1} + \dot C_{2} + \dot C_{0}[/math].

Запишем полученные выражения с учетом оператора а:

[math] \displaystyle \dot A = \dot A_{1} + \dot A_{2} + \dot A_{0}[/math];

[math] \displaystyle \dot B = \dot A_{1} \cdot \dot a^2 + \dot A_{2} \cdot \dot a + \dot B_{0}[/math];

[math] \displaystyle \dot C = \dot A_{1} \cdot \dot a + \dot A_{2} \cdot \dot a^2 + \dot C_{0}[/math].

Сложим эти уравнения, с учетом того, что [math] \displaystyle 1+\dot a+\dot a^2=0[/math] и получим:

[math] \displaystyle \dot A_{0} = \frac {1}{3} \cdot (\dot A + \dot B + \dot C)[/math].

Аналогичным образом выразим [math] \displaystyle \dot A_{1} \text { и } \dot A_{2}[/math]:

[math] \displaystyle \dot A_{1} = \frac {1}{3} \cdot (\dot A + \dot a \cdot \dot B + \dot a^2 \cdot \dot C)[/math];

[math] \displaystyle \dot A_{2} = \frac {1}{3} \cdot (\dot A + \dot a^2 \cdot \dot B + \dot a \cdot \dot C)[/math].

Таким образом можно записать матрицу Фортескью и свести задачу к матричной форме:

[math]\displaystyle \textbf{S} = \begin{pmatrix} 1 & 1 & 1 \\ 1 & \dot a^2 & \dot a \\ 1 & \dot a & \dot a^2 \end{pmatrix} \text { , } \begin{pmatrix} 1 & 1 & 1 \\ 1 & \dot a & \dot a^2 \\ 1 & \dot a^2 & \dot a \end{pmatrix}. [/math]

Матричная форма

[math] \displaystyle \mathbf {F}_{ЭВ} = \mathbf{S} \cdot \mathbf {F}_{CC} \text { или } \mathbf{F}_{CC} = \mathbf{S}^{-1} \cdot \mathbf{F}_{ЭВ}[/math],

где [math] \displaystyle \mathbf{F}_{ЭВ} \text { - фазный вектор произвольной величины, } \mathbf{F}_{CC} \text { - вектор симметричных составляющих.}[/math]

Разложение в действительных числах

В некоторых случаях при получении прямой, обратной и нулевой последовательности удобнее использовать не комплексную форму представления величин, а в виде компонент в прямоуголных координатах.

Прямая последовательность:

[math] \displaystyle X1' = \frac{1}{3} \left( Xa' - \frac{1}{2} Xb' - \frac{\sqrt{3}}{2} Xb'' - \frac{1}{2} Xc' + \frac{ \sqrt{3} }{2} Xc'' \right) [/math];

[math] \displaystyle X1''= \frac{1}{3} \left( Xa'' + \frac{ \sqrt{3} }{2} Xb' - \frac{1}{2} Xb'' - \frac{ \sqrt{3} }{2} Xc' - \frac{1}{2} Xc'' \right) [/math]; где

• [math]X1'[/math] - действительная часть вектора прямой последовательности;
• [math]X1''[/math] - мнимая часть вектора прямой последовательности;
• [math]Xa'[/math] - действительная часть вектора фазы А;
• [math]Xa''[/math] - мнимая часть вектора вектора фазы А;
• [math]Xb'[/math] - действительная часть вектора фазы В;
• [math]Xb''[/math] - мнимая часть вектора вектора фазы В;
• [math]Xc'[/math] - действительная часть вектора фазы C;
• [math]Xc''[/math] - мнимая часть вектора вектора фазы C.

Пример разложения

Рисунок 1. Векторная диаграмма разложения.

Пусть есть несимметричная система токов:

[math] \displaystyle \dot I_{A} = 2,791 \angle -23,277^\circ \text { A }[/math];

[math] \displaystyle \dot I_{B} = 4,281 \angle -144,316^\circ \text { A }[/math];

[math] \displaystyle \dot I_{C} = 1,934 \angle 50,077^\circ \text { A }[/math].

Найдем симметричные составляющие:

[math] \displaystyle \mathbf{I}_{CC} = \mathbf {S}^{-1} \cdot \mathbf{I}_{НС}[/math],

где [math] \displaystyle \mathbf{I}_{НС} \text { - фазный вектор исходных токов несеммитричной системы, } \mathbf{I}_{CC} \text { - вектор симметричных составляющих токов.}[/math]

[math]\displaystyle \mathbf{I}_{CC} = \begin{pmatrix} \dot I_{0} \\ \dot I_{1} \\ \dot I_{2} \end{pmatrix} = \begin{pmatrix} 2,791 \angle -23,277^\circ \\ 4,281 \angle -144,316^\circ \\ 1,934 \angle 50,077^\circ \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 & 1 \\ 1 & \dot a & \dot a^2 \\ 1 & \dot a^2 & \dot a \end{pmatrix} = \begin{pmatrix} 0,714 \angle -81,193^\circ \\ 2,843 \angle -33,295^\circ \\ 1,166 \angle 86,144^\circ \end{pmatrix} [/math]

Таким образом,

[math] \displaystyle \dot I_{A_{0}} = \dot I_{B_{0}} = \dot I_{C_{0}} = 0,714 \angle -81,193^\circ \text { A }[/math];

[math] \displaystyle \dot I_{A_{1}} = 2,843 \angle -33,295^\circ \text { A }[/math];

[math] \displaystyle \dot I_{B_{1}} = \dot I_{A_{1}} \cdot \dot a^2 = 2,843 \angle -153,295^\circ \text { A }[/math];

[math] \displaystyle \dot I_{C_{1}} = \dot I_{A_{1}} \cdot \dot a = 2,843 \angle 86,705^\circ \text { A }[/math];

[math] \displaystyle \dot I_{A_{2}} = 1,166 \angle 86,144^\circ \text { A }[/math];

[math] \displaystyle \dot I_{B_{2}} = \dot I_{A_{2}} \cdot \dot a = 1,166 \angle -153,856^\circ \text { A }[/math];

[math] \displaystyle \dot I_{C_{2}} = \dot I_{A_{2}} \cdot \dot a^2 = 1,166 \angle -33,856^\circ \text { A }[/math].

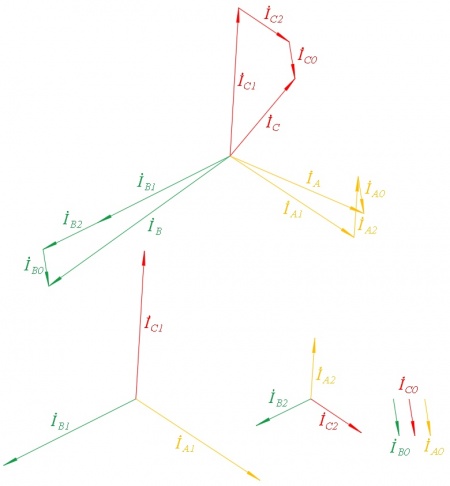
Векторная диаграмма разложения представленна на рисунке 1.

Рекомендуемая литература

• Ульянов С. А. Электромагнитные переходные процессы в электрических системах Учебник для электротехнических и энергетических ВУЗов и факультетов. М., «Энергия», 1970.
• Бессонов Л. А. Теоретические основы электротехники. Учебник для энергетических и электротехнических вузов и факультетов.