Идеальный трансформаторный двухполюсник — различия между версиями
(→Связь между мощностью начала и мощностью конца) |
Windsl (обсуждение | вклад) м (→Пример электрической схемы с трансформатором) |
||
| (не показаны 4 промежуточные версии 3 участников) | |||
| Строка 30: | Строка 30: | ||
Рассмотрим первое [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%B0_%D0%9A%D0%B8%D1%80%D1%85%D0%B3%D0%BE%D1%84%D0%B0 правило Кирхгофа] для узла 1: | Рассмотрим первое [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%B0_%D0%9A%D0%B8%D1%80%D1%85%D0%B3%D0%BE%D1%84%D0%B0 правило Кирхгофа] для узла 1: | ||
| − | : <math>\dot{I}_{\text{вход}} = \dot{I}_1 + \dot{I}_2</math>. | + | : <math>\displaystyle\dot{I}_{\text{вход}} = \dot{I}_1 + \dot{I}_2</math>. |
Для второго узла соответственно: | Для второго узла соответственно: | ||
| − | : <math>\dot{I}_{\text{выход}} = \dot{I}_1 + \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>. | + | : <math>\displaystyle\dot{I}_{\text{выход}} = \dot{I}_1 + \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>. |
С учётом того, что ток на входе схемы и на выходе равны друг другу <math>\dot{I}_{\text{вход}} = \dot{I}_{\text{выход}}</math><ref>Теоретические основы электротехники. Учебник для вузов. 5-е изд. Том 1. Нейман Л. Р., Коровкин Н. В., Демирчян К. С. ISBN 978-5-388-00410-9. стр. 165, п.3.15</ref>, то получается следующее равенство: | С учётом того, что ток на входе схемы и на выходе равны друг другу <math>\dot{I}_{\text{вход}} = \dot{I}_{\text{выход}}</math><ref>Теоретические основы электротехники. Учебник для вузов. 5-е изд. Том 1. Нейман Л. Р., Коровкин Н. В., Демирчян К. С. ISBN 978-5-388-00410-9. стр. 165, п.3.15</ref>, то получается следующее равенство: | ||
| − | : <math>\dot{I}_1 + \dot{I}_2 = I_1 + \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>. | + | : <math>\displaystyle\dot{I}_1 + \dot{I}_2 = I_1 + \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>. |
И далее получаем: | И далее получаем: | ||
| − | : <math> \dot{I}_2 = \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>. | + | : <math>\displaystyle \dot{I}_2 = \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>. |
С другой стороны, ток на входе идеального трансформатрного двухполюсника не равен току на выходе: | С другой стороны, ток на входе идеального трансформатрного двухполюсника не равен току на выходе: | ||
| − | : <math> \dot{I}_2 \ne \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>, | + | : <math>\displaystyle \dot{I}_2 \ne \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2</math>, |
| − | так как <math> \stackrel{\ast}{k}_{\text{тр}} \ne 1</math>. | + | так как <math>\displaystyle \stackrel{\ast}{k}_{\text{тр}} \ne 1</math>. |
Отсюда следует, что наличие в схеме идеального трансформаторного двухполюсника приводит к нарушению правила Кирхгофа в токах для группы узлов <math>\dot{I}_{\text{вход}} \ne \dot{I}_{\text{выход}}</math>. При этом в мощностях правило Кирхгофа для группы узлов всё ещё справедливо: | Отсюда следует, что наличие в схеме идеального трансформаторного двухполюсника приводит к нарушению правила Кирхгофа в токах для группы узлов <math>\dot{I}_{\text{вход}} \ne \dot{I}_{\text{выход}}</math>. При этом в мощностях правило Кирхгофа для группы узлов всё ещё справедливо: | ||
| − | : <math>\dot{S}_{\text{вход}} = \dot{S}_{\text{выход}} + \Delta \dot{S}_{\text{ветвь1}} + \Delta \dot{S}_{\text{ветвь2}}</math>. | + | : <math>\displaystyle\dot{S}_{\text{вход}} = \dot{S}_{\text{выход}} + \Delta \dot{S}_{\text{ветвь1}} + \Delta \dot{S}_{\text{ветвь2}}</math>. |
| + | |||
| + | Этот парадокс возникает вследствие того, что трансформатор представлен в виде двухполюсника в однолинейной схеме замещения. В случае, если представить однофазный трансформатор в виде четырёхполюсника, то данный парадокс не возникает. | ||
Однако [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%B0_%D0%9A%D0%B8%D1%80%D1%85%D0%B3%D0%BE%D1%84%D0%B0 второй закон Кирхгофа] для данного случая справедлив. Рассмотрим следующую схему: | Однако [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%B0_%D0%9A%D0%B8%D1%80%D1%85%D0%B3%D0%BE%D1%84%D0%B0 второй закон Кирхгофа] для данного случая справедлив. Рассмотрим следующую схему: | ||
| Строка 58: | Строка 60: | ||
[[Файл:Secondpart.jpg|600px|]] | [[Файл:Secondpart.jpg|600px|]] | ||
| − | По второму закону Кирхгофа <math>\sum_{i=1}^{N} | + | По второму закону Кирхгофа <math>\displaystyle\sum_{i=1}^{N}U_{i}=\sum_{i=1}^{N}e_{i}</math>, |
| − | в нашем случае имеем: <math>\Delta\dot{ | + | в нашем случае имеем: <math>\displaystyle\Delta\dot{U}_{12}-\Delta\dot{U}_{23}-\Delta\dot{U}_{13}=0</math> или <math>\Delta\dot{U}_{12}=\Delta\dot{U}_{23}+\Delta\dot{U}_{13}</math>, где |
| − | : <math>\Delta\dot{ | + | : <math>\displaystyle\Delta\dot{U}_{12}=\dot{U}_{1}-\dot{U}_{2}</math>, |
| − | : <math>\Delta\dot{ | + | : <math>\displaystyle\Delta\dot{U}_{13}=\dot{U}_{1}-\dot{U}_{3}=\left[\dot{k} = \frac{\dot{U}_{3}}{\dot{U}_{1}}\right] = \dot{U}_{1}-\dot{k} \cdot \dot{U}_{1} = \dot{U}_{1}\left(1-\dot{k}\right)</math>, |
| − | : <math>\Delta\dot{ | + | : <math>\displaystyle\Delta\dot{U}_{23}=\dot{U}_{3}-\dot{U}_{2}=\dot{k} \cdot \dot{U}_{1}-\dot{U}_{2}</math>, |
получаем, что: | получаем, что: | ||
| − | : <math>\dot{ | + | : <math>\displaystyle\dot{U}_{1}-\dot{U}_{2} = \left(\dot{k} \cdot \dot{U}_{1}-\dot{U}_{2}\right)+\left(\dot{U}_{1}-\dot{k} \cdot \dot{U}_{1}\right)\Longrightarrow\dot{U}_{1}-\dot{U}_{2} = -\dot{U}_{2}+\dot{U}_{1}</math>, |
левая часть уравнения равна правой части, отсюда следует, что второй закон Кирхгофа выполняется. | левая часть уравнения равна правой части, отсюда следует, что второй закон Кирхгофа выполняется. | ||
| − | |||
| − | |||
= Использованные источники = | = Использованные источники = | ||
[[Категория:Схемы замещения]] | [[Категория:Схемы замещения]] | ||
Текущая версия на 19:08, 21 марта 2019
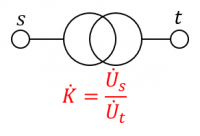
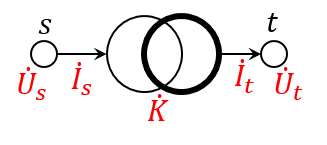
Идеальный трансформаторный двухполюсник — это направленный двухполюсник электрической сети (узел начала будем обозначать, как [math]s[/math] «source», а узел конца — как [math]t[/math]) «target», параметром которого является ненулевой (в общем случае, комплексный) коэффициент [math]\dot{K} \neq 0[/math], называемый коэффициент трансформации, и для которого всегда истинно:
- [math]\dot{U}_s = \dot{K} \cdot {\dot{U}_t};[/math]
- [math]\dot{I}_t = \stackrel{\ast}{K} \cdot \dot{I}_s.[/math]
Содержание
Обозначение на схеме
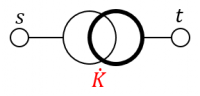
Ни учебники, ни стандарты, ни монографии не регламентируют, как именно обозначать на схеме узел начала и узел конца. Чаще всего, направление двухполюсника определяется из контекста задачи, либо явно прописываются тем, или иным образом. В данной статье предлагается круг, относящийся к стороне узла конца делать жирнее круга, относящегося к узлу начала, для ликвидации симметричности обозначения. Когда применено стандартное обозначение, следует идентифицировать начало и конец исходя из контекста.
Связь между мощностью начала и мощностью конца
Исходя из определения комплексной мощности:
- [math]\displaystyle\dot{S}_s = \dot{U}_s \cdot \overset{\ast}{I}_s;[/math]
- [math]\displaystyle\dot{S}_t = \dot{U}_t \cdot \overset{\ast}{I}_t.[/math]
Подставим соотношения напряжений начала и конца двухполюсника в определение мощности начала
- [math]\displaystyle\dot{S}_s = \dot{U}_s \cdot \overset{\ast}{I}_s = \dot{K} \cdot {\dot{U}_t} \cdot \overset{\ast}{I}_s.[/math]
Подставим соотношения токов начала и конца двухполюсника в определение мощности конца
- [math]\displaystyle\dot{S}_t = \dot{U}_t \cdot \overset{\ast}{I}_t = \dot{K} \cdot {\dot{U}_t} \cdot \overset{\ast}{I}_s = {\dot{U}_s} \cdot \overset{\ast}{I}_s.[/math]
Следовательно, для идеального трансформаторного двухполюсника всегда истинно:
- [math]\displaystyle\dot{S}_s = \dot{S}_t.[/math]
Пример электрической схемы с трансформатором
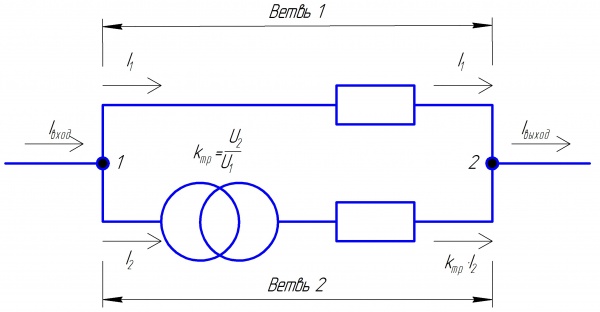
В качестве примера для размышления о влиянии идеального трансформаторного двухполюсника на параметры электрического режима можно привести следующую схему:
Рассмотрим первое правило Кирхгофа для узла 1:
- [math]\displaystyle\dot{I}_{\text{вход}} = \dot{I}_1 + \dot{I}_2[/math].
Для второго узла соответственно:
- [math]\displaystyle\dot{I}_{\text{выход}} = \dot{I}_1 + \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2[/math].
С учётом того, что ток на входе схемы и на выходе равны друг другу [math]\dot{I}_{\text{вход}} = \dot{I}_{\text{выход}}[/math][1], то получается следующее равенство:
- [math]\displaystyle\dot{I}_1 + \dot{I}_2 = I_1 + \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2[/math].
И далее получаем:
- [math]\displaystyle \dot{I}_2 = \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2[/math].
С другой стороны, ток на входе идеального трансформатрного двухполюсника не равен току на выходе:
- [math]\displaystyle \dot{I}_2 \ne \stackrel{\ast}{k}_{\text{тр}} \cdot \dot{I}_2[/math],
так как [math]\displaystyle \stackrel{\ast}{k}_{\text{тр}} \ne 1[/math].
Отсюда следует, что наличие в схеме идеального трансформаторного двухполюсника приводит к нарушению правила Кирхгофа в токах для группы узлов [math]\dot{I}_{\text{вход}} \ne \dot{I}_{\text{выход}}[/math]. При этом в мощностях правило Кирхгофа для группы узлов всё ещё справедливо:
- [math]\displaystyle\dot{S}_{\text{вход}} = \dot{S}_{\text{выход}} + \Delta \dot{S}_{\text{ветвь1}} + \Delta \dot{S}_{\text{ветвь2}}[/math].
Этот парадокс возникает вследствие того, что трансформатор представлен в виде двухполюсника в однолинейной схеме замещения. В случае, если представить однофазный трансформатор в виде четырёхполюсника, то данный парадокс не возникает.
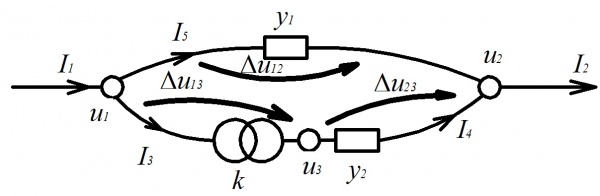
Однако второй закон Кирхгофа для данного случая справедлив. Рассмотрим следующую схему:
По второму закону Кирхгофа [math]\displaystyle\sum_{i=1}^{N}U_{i}=\sum_{i=1}^{N}e_{i}[/math],
в нашем случае имеем: [math]\displaystyle\Delta\dot{U}_{12}-\Delta\dot{U}_{23}-\Delta\dot{U}_{13}=0[/math] или [math]\Delta\dot{U}_{12}=\Delta\dot{U}_{23}+\Delta\dot{U}_{13}[/math], где
- [math]\displaystyle\Delta\dot{U}_{12}=\dot{U}_{1}-\dot{U}_{2}[/math],
- [math]\displaystyle\Delta\dot{U}_{13}=\dot{U}_{1}-\dot{U}_{3}=\left[\dot{k} = \frac{\dot{U}_{3}}{\dot{U}_{1}}\right] = \dot{U}_{1}-\dot{k} \cdot \dot{U}_{1} = \dot{U}_{1}\left(1-\dot{k}\right)[/math],
- [math]\displaystyle\Delta\dot{U}_{23}=\dot{U}_{3}-\dot{U}_{2}=\dot{k} \cdot \dot{U}_{1}-\dot{U}_{2}[/math],
получаем, что:
- [math]\displaystyle\dot{U}_{1}-\dot{U}_{2} = \left(\dot{k} \cdot \dot{U}_{1}-\dot{U}_{2}\right)+\left(\dot{U}_{1}-\dot{k} \cdot \dot{U}_{1}\right)\Longrightarrow\dot{U}_{1}-\dot{U}_{2} = -\dot{U}_{2}+\dot{U}_{1}[/math],
левая часть уравнения равна правой части, отсюда следует, что второй закон Кирхгофа выполняется.
Использованные источники
- ↑ Теоретические основы электротехники. Учебник для вузов. 5-е изд. Том 1. Нейман Л. Р., Коровкин Н. В., Демирчян К. С. ISBN 978-5-388-00410-9. стр. 165, п.3.15